Turbomáquinas e Bodé

 Uma medição importante feita utilizando a capacidade de seguimento de ordens dos analisadores de vibrações é a dos arranques e paragens de turbomáquinas e Bodé.

Este artigo pertence a uma série, que constitui o material de suporte do curso de análise de vibrações em turbomáquinas. As ligações para os outros artigos podem ser encontradas aqui.

Importância dos dados adquiridos em regime transitório

Em muitas máquinas, a única vez que operam em determinadas velocidades importantes (ou seja. velocidades críticas, em ressonâncias estruturais, etc.) é durante um arranque ou paragem.

A vibração em regime transiente fornece uma grande quantidade de informação que não está disponível a partir de dados em estado estacionário. Entre elas estão:

• A capacidade de comparar a amplitude da vibração, a fase, a posição do veio, etc., a velocidades acima e abaixo das velocidades críticas do veio
• A melhor assinatura das frequências naturais globais do rotor, que são normalmente o resultado da relação complexa entre os suportes do rotor do rotor (chumaceiras, vedantes, etc.) e a natureza dinâmica do próprio rotor

Tão importante quanto as comparações listadas acima é a capacidade de comparar dados transientes antes e depois da existência de um problema na máquina. As avaliações do estado das máquinas são muito mais fáceis quando se dispõe da capacidade de comparar o antes e o depois.

Do mesmo modo, é muito importante avaliar muitos tipos diferentes de gráficos para apresentar dados de vibrações. A utilização de apenas um tipo de gráfico limita a capacidade do especialista em máquinas de obter uma “imagem” adequada do estado da máquina.

Esta medida é uma indicação importante da condição das máquinas e é usada geralmente para qualificar máquinas de alta velocidade novas ou após revisão. A medição usa o desequilíbrio residual na máquina para excitá-la a diferentes frequências, uma vez que funciona até à velocidade operacional e mede a resposta (magnitude e fase) em função da velocidade. Isto utiliza a capacidade básica de seguimento de ordens do analisador de vibrações juntamente com recursos especiais de apresentação de resultados desta medição.

O Bodé

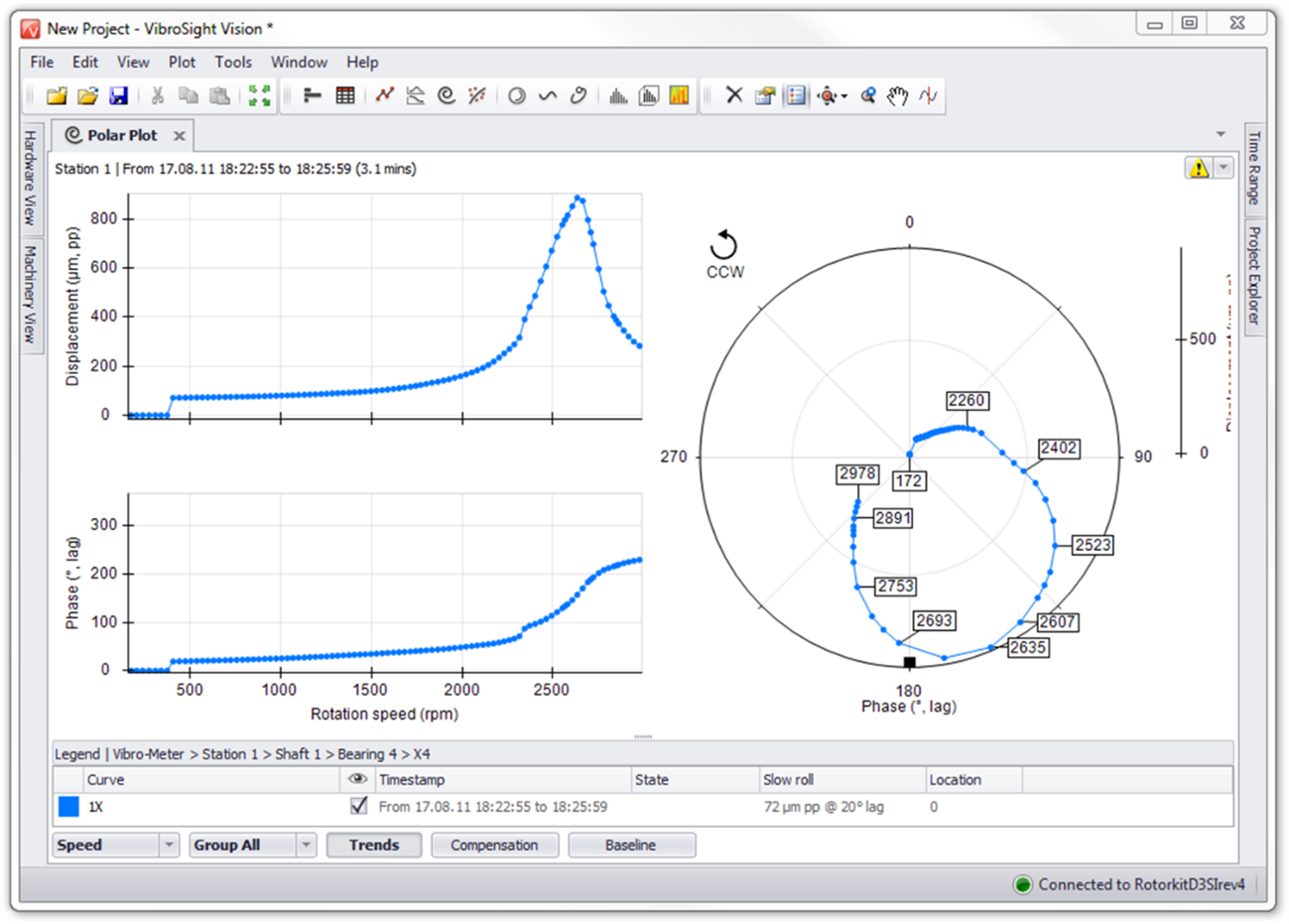
Os gráficos de Bodé são um método comum de exibição de dados transitórios. Normalmente exibem vibração global ou síncrona (no entanto, os dados nX também podem ser exibidos) e fase correspondente, versus velocidade de rotação.

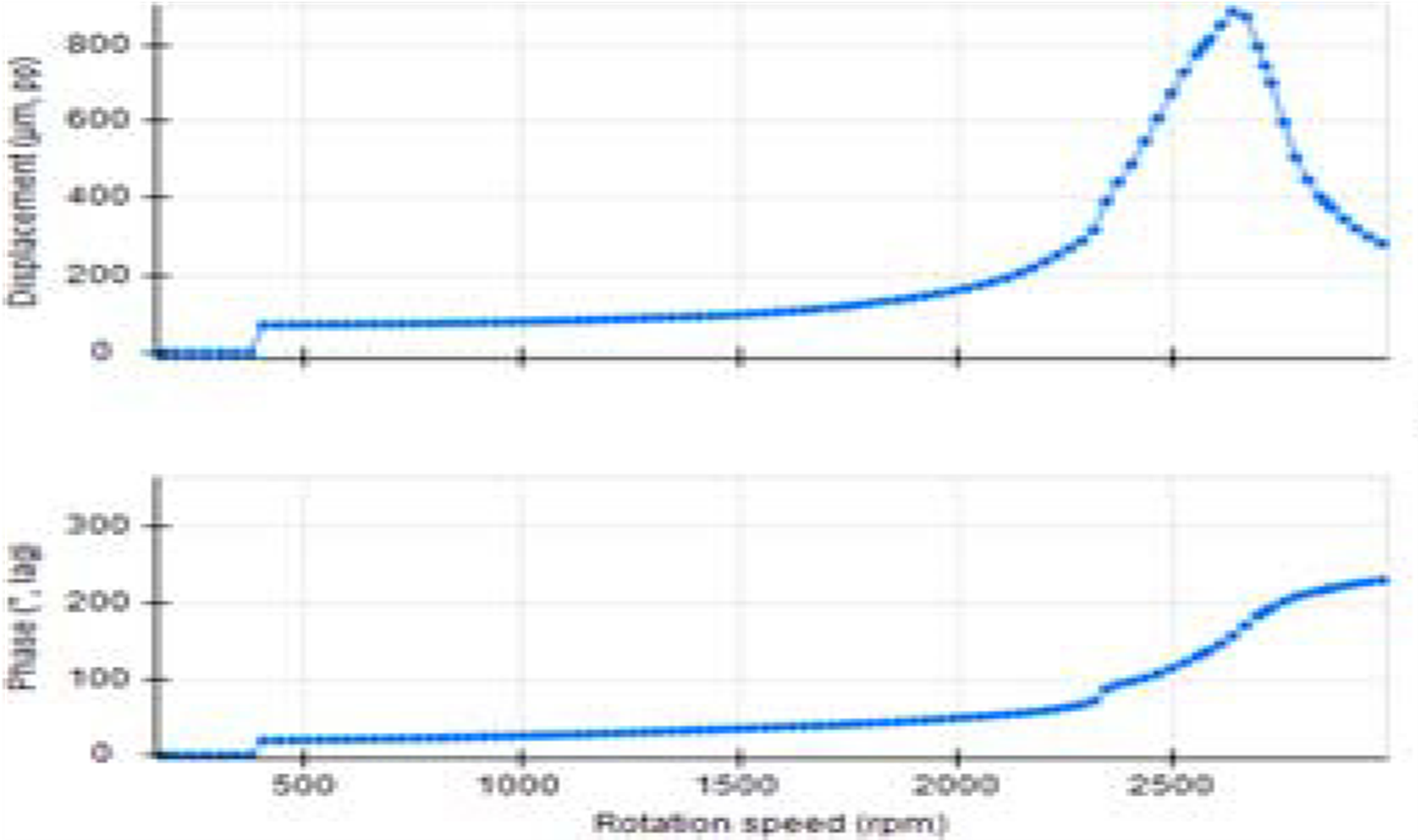
Turbomáquinas e Bodé – Figura 1– O Diagrama de BODÉ do arranque de uma máquina, mostrando as velocidades críticas. O gráfico superior mostra nível de vibrações, o do meio o da fase e o de baixo a velocidade de rotação. O nível de vibrações e a fase são apresentados em função 1 x RPM

Um benefício dos analisadores de vibrações nesta medida, é sua capacidade de seguir simultaneamente várias ordens e exibi-las, além da velocidade de rotação fundamental (1ª ordem); bem como o nível geral e o perfil rpm como se vê na figura.

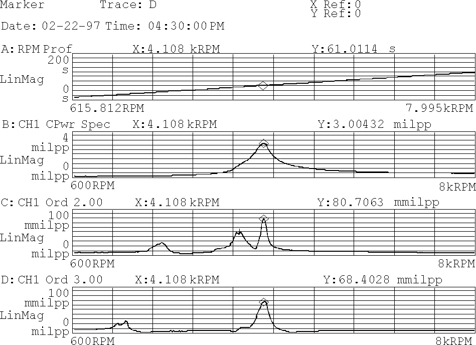
Turbomáquinas e Bodé – Figura 2– Diagrama de BODÉ do arranque de uma máquina, com apresentação da 2ª e 3ª ordem, assim como o nível global e a RPM da máquina.

As frequências naturais do rotor podem ser determinadas localizando o pico na amplitude de vibração que corresponde também a uma mudança de fase de aproximadamente 180 graus.

Os gráficos polares mostram os mesmos dados que os gráficos de Bodé, apenas em um formato diferente. Às vezes, os gráficos polares facilitam a determinação de quando o rotor cruzou sua velocidade crítica, porque a mudança de fase é óbvia (ou seja, a cada 180 graus no gráfico). Por exemplo, a partir do gráfico de Bodé mostrado na anterior, não é imediatamente óbvio que este rotor está se aproximando da segunda velocidade crítica. No entanto, no gráfico polar isto é muito claro.

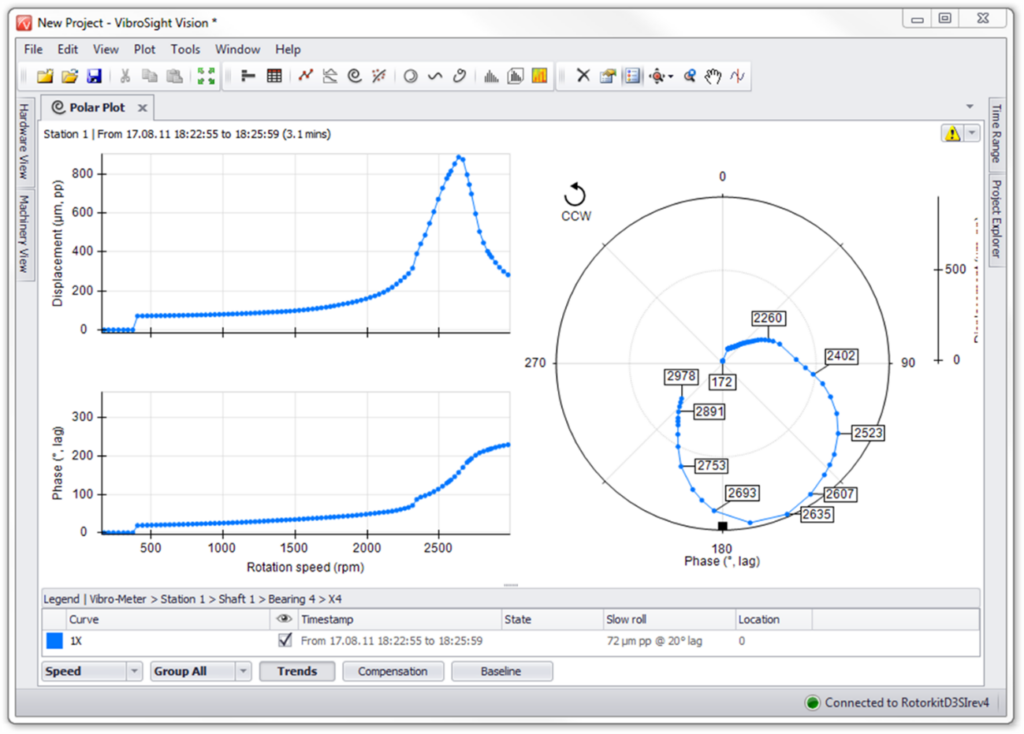
Turbomáquinas e Bodé – Figura 3

Os gráficos de Bodé e o Polar podem ser compensados ​​por excentricidade (run-out). Todas as áreas onde o proximitor mede têm uma certa quantidade de desvio físico e/ou elétrico. Os dados vetoriais são corrigidos para esta excentricidade subtraindo vectorialmente o vetor de vibração a uma rpm muito baixa de todos os dados vetoriais obtidos.

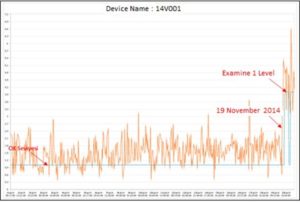
Exemplo de ressonância identificada com o Bodé

Este diagrama de Bodé evidencia duas frequências de ressonância, a primeira a 2200 RPM, que não afeta o funcionamento da máquina. A segunda, está a 3515 RPM que é a velocidade de rotação da máquina originando um fenómeno de ressonância.

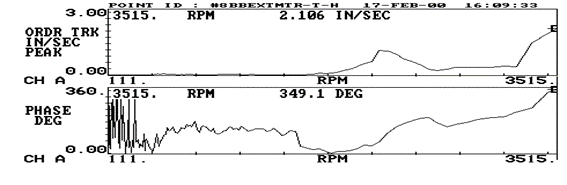
Turbomáquinas e Bodé – Figura 4

Turbomáquinas e Bodé – Compreender o diagrama de Bodé

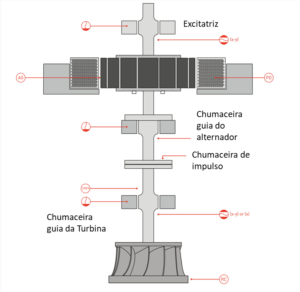
O rotor de Laval-Jeff

É necessária uma compreensão básica da dinâmica de rotores para melhor interpretar os dados de vibração transiente. O rotor de Laval-Jeffcott fornece um modelo simplificado de um rotor entre chumaceiras, como se vê na Figura 1. Neste modelo a rigidez reside toda no veio e a massa reside toda o disco.

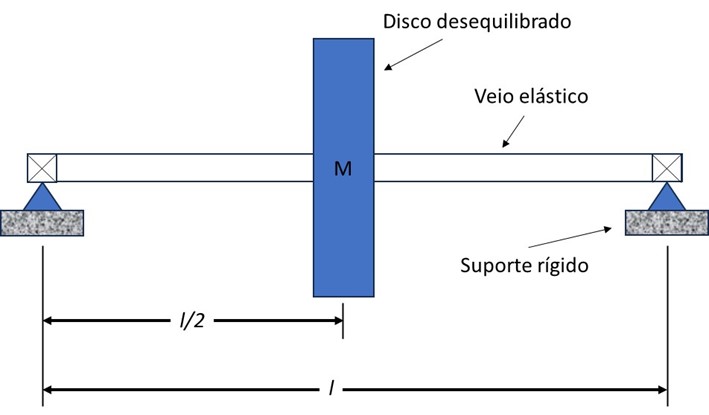
Turbomáquinas e Bodé – Figura 5 – O rotor Laval-Jeffcott

O disco desequilibrado está localizado no centro do rotor sem massa sobre suportes rígidos. O único amortecimento no sistema é devido à resistência viscosa do ar. Embora o rotor Laval-Jeffcott seja um modelo muito simples, ele pode fornecer uma grande quantidade de informações sobre os efeitos da vibração síncrona em turbomáquinas. Uma vista de topo do rotor Laval-Jeffcott mostra a relação entre o centro de massa (M) e o centro geométrico (C).

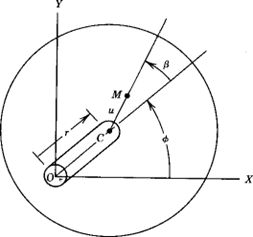
u	= raio de desequilíbrio
C	= centro geométrico
β	= ângulo de fase síncrono
M	= centro de massa do desequilíbrio

Turbomáquinas e Bodé – Figura 6 – Vista de topo do rotor Laval-Jeffcott.

Resposta do rotor de Laval-Jeff em amplitude e fase relativamente a um desequilíbrio

O ângulo de fase síncrono (β) é a diferença entre o vetor de desequilíbrio (U) e o vetor de deslocamento (R). A amplitude de rotação síncrona e o ângulo de fase para o rotor Laval-Jeffcott à medida que este passa pela primeira ressonância do rotor (velocidade crítica) são apresentados na Figura 3.

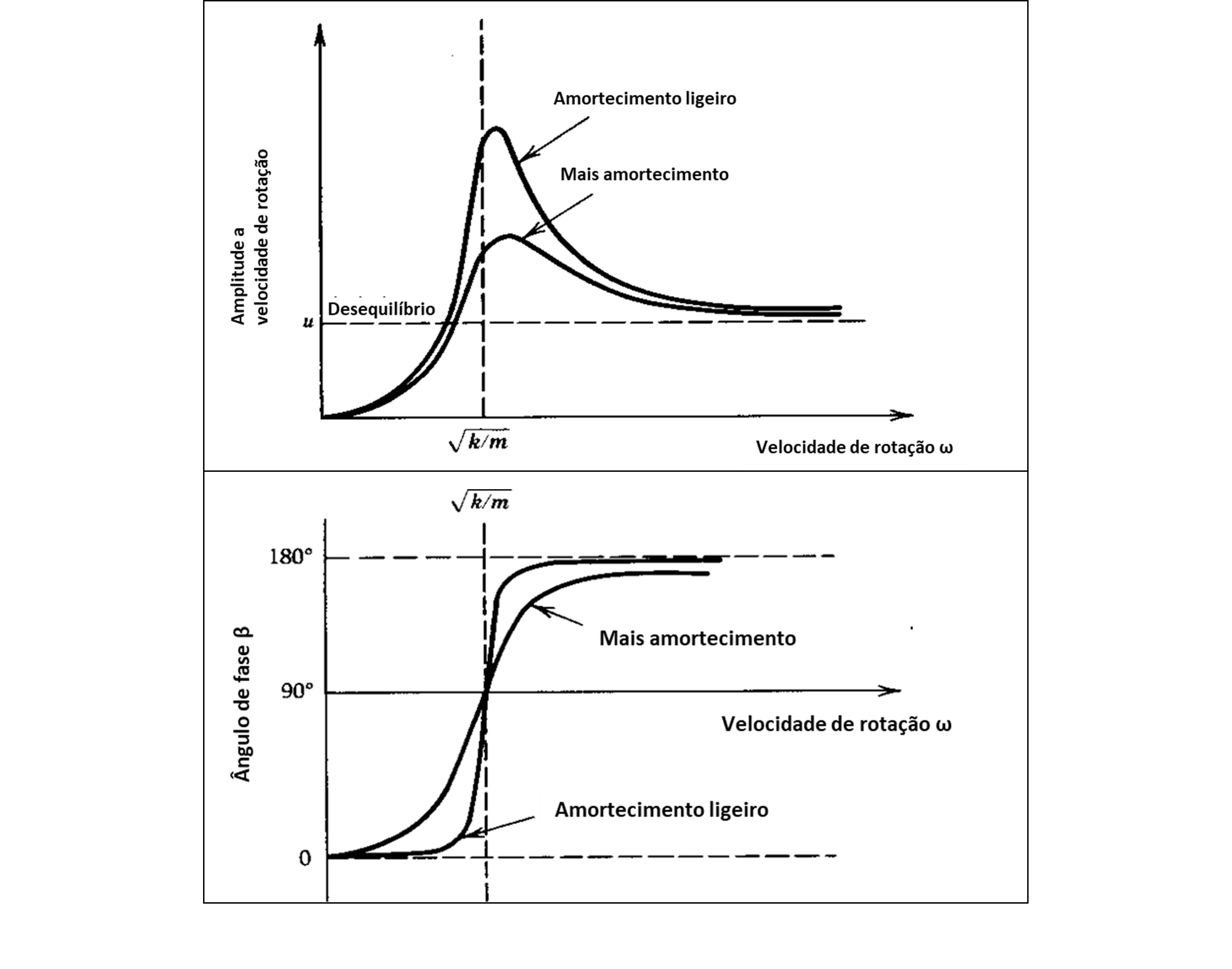
Turbomáquinas e Bodé – Figura 7. Resposta síncrona e ângulo de fase do rotor Laval-Jeffcott.

A equação da amplitude de resposta é apresentada na Equação (1).

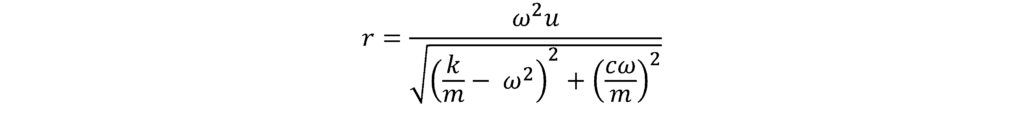
Uma explicação física destes gráficos mostra que:

• Muito abaixo da velocidade crítica, o vetor de resposta R e o vetor de desequilíbrio U estão em fase (i.e., β ~ 0).
• À medida que a velocidade de rotação aumenta, o vetor de desequilíbrio U começa a liderar R.
• À medida que a velocidade crítica é ultrapassada, β passa por 90 graus e depois aproxima-se assintoticamente de 180 graus a velocidades acima da crítica.
• Assim, a velocidades muito acima da velocidade crítica, o centro de massa do rotor (M) desloca-se para o centro da órbita da rotação e fica parado, enquanto o centro do veio gira em torno do centro de massa.

Assim tem-se como se vê na figura a seguir.

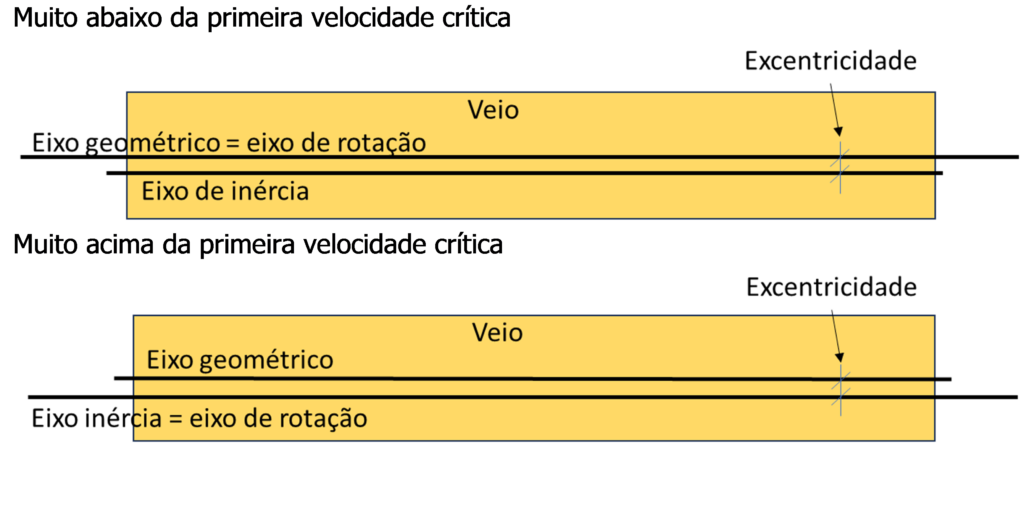
Turbomáquinas e Bodé – Figura 8

Turbomáquinas e Bodé – Significado físico da variação de fase

Como se explica então que a partir da velocidade crítica não se veja o efeito do aumento da força centrifuga por efeito do aumento da velocidade de rotação?

Repetindo, a velocidades muito acima da velocidade crítica:

• O centro de massa do rotor (M) desloca-se para o centro da órbita da rotação e fica parado,
• Enquanto o centro do veio gira em torno do centro de massa.

Veja-se o vídeo:

Vê-se que acima da primeira frequência natural a mola não transmite força suficiente (não e suficientemente rígida) para mover a massa e é como se esta se recusasse a mover, devido à sua inércia.

Por outras palavras, muita acima da velocidade critica a força de inercia é maior que a força de rigidez que a mola consegue transmitir, como se pode ver na figura a seguir.

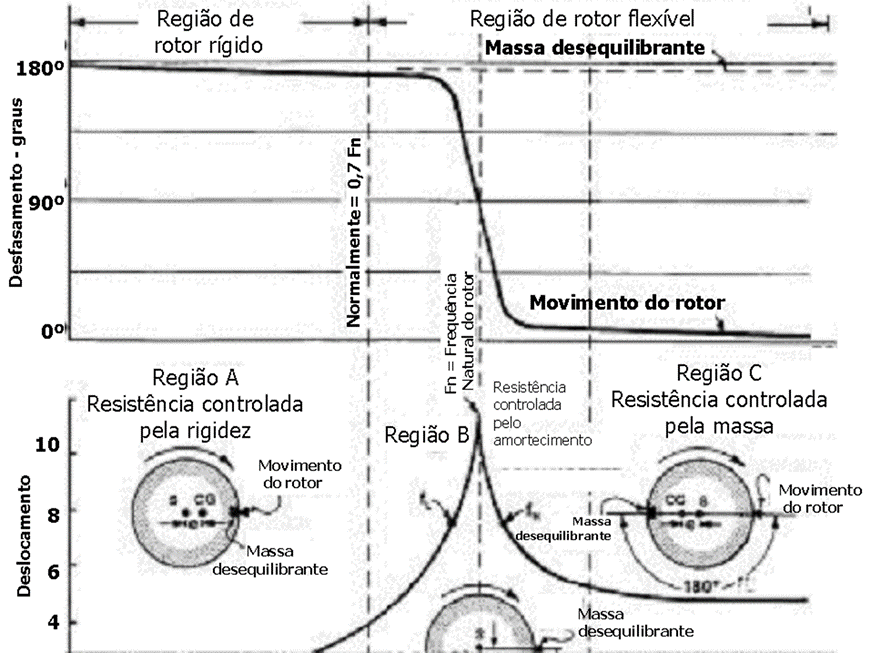
Turbomáquinas e Bodé – Figura 9

Ou seja, muito acima da velocidade crítica o veio roda em torno do centro de massa. A amplitude do movimento corresponde à excentricidade entre o eixo de inércia e o eixo geométrico.

Resposta do rotor de Laval-Jeff em amplitude e fase a forças não dependentes da frequência

Adicionalmente, o efeito que as forças não dependentes da frequência têm na amplitude da rotação é mostrado na Figura.

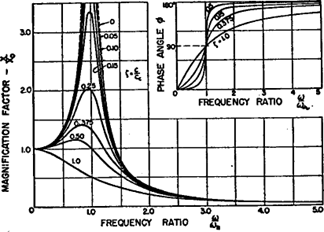
Turbomáquinas e Bodé – Figura 10 – Resposta síncrona a uma força constante, ou seja, por exemplo, desalinhamento.

A resposta síncrona efetiva será uma combinação das Figuras 6 e 10.

Relação entre as forças de rigidez, amortecimento e desequilíbrio para o rotor Laval-Jeffcott

A figura 11 a seguir apresenta uma ilustração das forças de rigidez, de amortecimento e de desequilíbrio para o rotor Laval-Jeffcott a velocidades abaixo, em, e acima da primeira ressonância de equilíbrio.

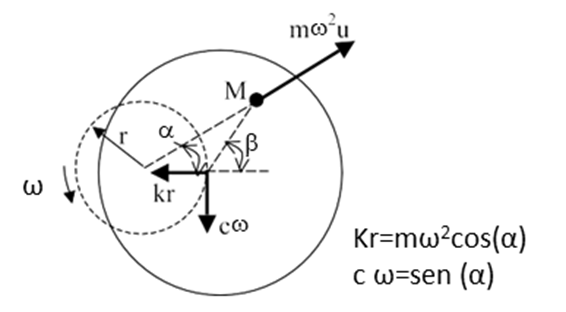
Turbomáquinas e Bodé – Figura 11 – Resposta síncrona abaixo, na, e acima da velocidade crítica.

Desta forma, a relação entre as forças de rigidez, amortecimento e inércia, nas diferentes velocidades, é a que se pode ver na Tabela I a seguir apresentada.

Tabela I Relação entre as forças de rigidez, amortecimento e inércia, nas diferentes velocidades

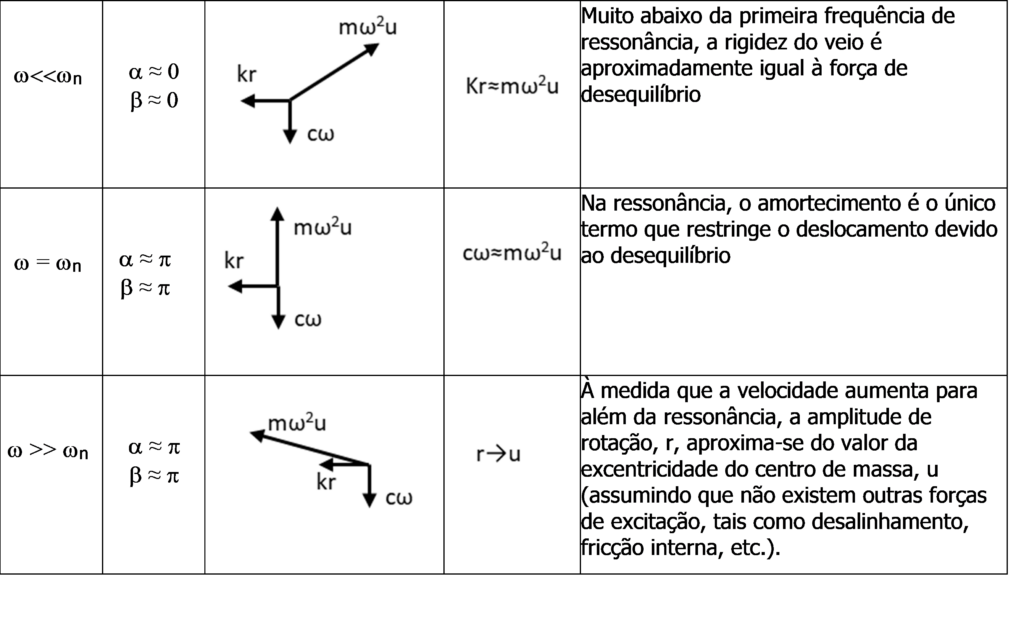
Como se pode ver, muito abaixo da primeira frequência de ressonância, a rigidez do veio é aproximadamente igual à força de desequilíbrio. No entanto, na ressonância, o amortecimento é o único termo que restringe o deslocamento devido ao desequilíbrio. Da mesma forma, à medida que a velocidade aumenta para além da ressonância, a amplitude de rotação, r, aproxima-se do valor da excentricidade do centro de massa, u (assumindo que não existem outras forças de excitação, tais como desalinhamento, fricção interna, etc.).

Turbomáquinas e Bodé – Quantidade de amortecimento no sistema do rotor -Q

Uma vez que na ressonância, o amortecimento é a única força que contém o deslocamento do rotor Laval-Jeffcott, a medição do deslocamento à medida que o rotor passa pela ressonância é um bom método para determinar a quantidade de amortecimento no sistema do rotor.

O fator de amplificação síncrona (Q) é uma medida da severidade de uma ressonância, bem como uma indicação do amortecimento presente. Embora existam vários métodos disponíveis para medir Q, o método de meia potência é utilizado aqui porque é o mais amplamente aceite. A definição básica é dada a seguir na Equação (2)

A largura de banda de frequência é a diferença entre as frequências em que a amplitude é 3 dB inferior ao máximo no pico de ressonância. Isto corresponde a 0,707 vezes a amplitude na ressonância. Este método foi adotado pelo American Petroleum Institute (API) para medir o fator de amplificação síncrono.

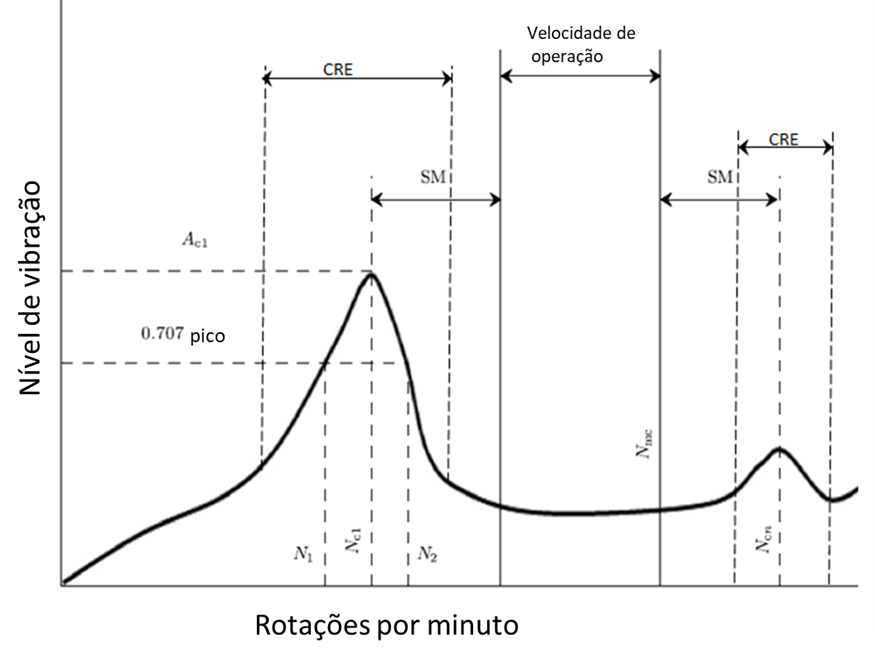
Nc1	= Centro de frequência da primeira velocidade crítica (ciclos por minuto)
Ncn	= Velocidade critica
Nmc	= Máxima velocidade continua, 105 por cento
N1	= Velocidade inferior, a 0,707x a amplitude pico da velocidade crítica
N2	= Velocidade superior, a 0,707x a amplitude pico da velocidade crítica
N1-N2	= Largura do pico com nível a metade da potência
Q	= Fator de amplificação =
SM	= Margem de separação
CRE	= Envelope de resposta crítica
Ac1	= Nível a NC1
Acn	= Nível a NCn

Turbomáquinas e Bodé – Figura 12 – Definição de Fator de Amplificação Síncrona de acordo com o API 617.

Em geral:

• As máquinas com fatores de amplificação síncrona inferiores a quatro são consideradas muito bem amortecidas.
• Valores entre quatro e oito são considerados adequadamente amortecidos e são normalmente estáveis.
• Entre oito e 15 são considerados marginais, embora muitas máquinas mais antigas possam operar na área.
• Os fatores de amplificação acima de 15 são considerados como tendo amortecimento insuficiente e são muito suscetíveis de apresentar fricções no arranque e problemas de estabilidade.

O fator de amplificação síncrona é um parâmetro de diagnóstico importante para avaliar a estabilidade da máquina e comparar o estado da máquina antes e depois da existência de um problema no equipamento. Como se pode ver na Figura 3, o fator de amplificação aumenta à medida que o amortecimento do sistema diminui. Uma vez que a maior parte do amortecimento em máquinas de alta velocidade provém das chumaceiras hidrodinâmicas, as alterações no fator de amplificação síncrona podem indicar uma alteração no amortecimento fornecido pelas chumaceiras. O que, por sua vez, pode indicar uma mudança no estado das chumaceiras.

O rotor Laval-Jeffcott com apoios de chumaceiras flexíveis

Uma vez que a maior parte das turbomáquinas é apoiada em chumaceiras hidrodinâmicas, os efeitos dos apoios flexíveis também têm de ser considerados. O rotor Laval-Jeffcott pode ser modificado para ter apoios de chumaceiras flexíveis (Figura 7).

Turbomáquinas e Bodé – Figura 13 – Rotor Laval-Jeffcott com suportes flexíveis

Os suportes flexíveis são desejáveis do ponto de vista da dinâmica de rotores porque:

• Podem reduzir a carga dinâmica transmitida à carcaça;
• Permitem que o amortecimento nos apoios seja mais eficaz (ou seja, apoios menos rígidos permitem mais velocidade nos apoios, o que é necessário para o amortecimento).

Relação entre a força gerada e a força transmitida – Transmissibilidade

O rácio de transmissibilidade calculado (F_B/F_x) para diferentes valores de amortecimento é apresentado na Figura 8.

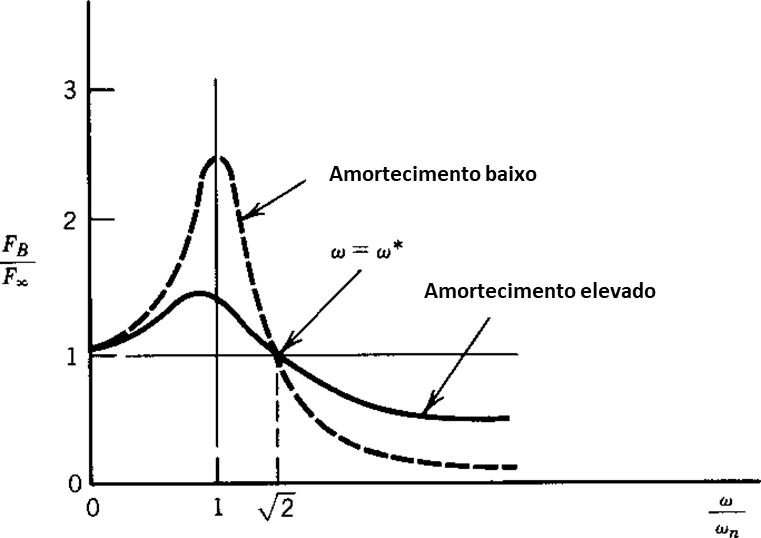
Turbomáquinas e Bodé – Figura 14 – Transmissibilidade versus relação de velocidade do veio com velocidade crítica

Como se pode ver, o amortecimento reduz a força transmitida às chumaceiras em ressonância, mas na realidade faz com que seja maior para ω/ω_n > 1,14. Isto contrasta com a Figura 3, onde o amortecimento tem um efeito desejável na amplitude da rotação para toda a gama de velocidades. De um modo geral, é desejável (do ponto de vista da resposta síncrona e da estabilidade) que a relação entre a rigidez da chumaceira e a do veio (K_B/K_veio) seja tão baixa quanto possível, com a restrição óbvia de que a baixa rigidez da chumaceira não deve fazer com que a máquina funcione mais perto de uma ressonância.

Direções da rigidez do suporte do rotor

Além disso, a rigidez do suporte do rotor nem sempre está na direção principal (isto é, a rigidez principal produz uma força oposta à direção do deslocamento do rotor). Os coeficientes de rigidez e de amortecimento de um suporte de chumaceira ou de vedantes podem ser divididos da seguinte forma .

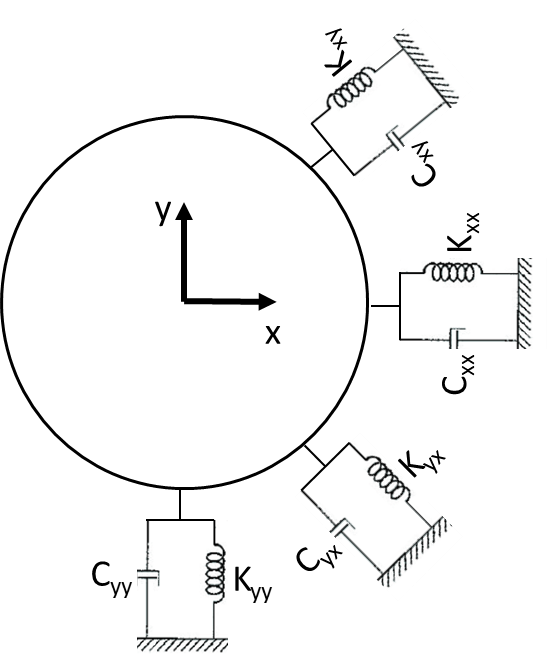
Turbomáquinas e Bodé – Figura 15 – Coeficientes de rigidez e de amortecimento de suportes.

5 – Coeficientes de rigidez e de amortecimento de suportes.

Os termos K_xy e K_yx são normalmente designados por termos de “acoplamento cruzado” (se o veio for deslocado na direção vertical, a rigidez de acoplamento cruzado produz uma força de reação na direção horizontal) e reduzem os efeitos positivos do amortecimento se K_xy (-K_yx) > 0. Por esta razão, quando K_xy > 0, o fator de amplificação do rotor aumenta e a estabilidade é reduzida. A equação (3) dá a resposta de um rotor rígido sobre apoios flexíveis, incluindo os efeitos de acoplamento cruzado. Note-se que quando K_xy > 0, reduz o termo de amortecimento e aumenta o fator de amplificação. Por esta razão, quando o fator de amplificação é medido a partir de dados de campo, é na realidade uma medida da combinação do amortecimento direto e da rigidez de acoplamento cruzado presentes na máquina.

Desequilíbrio, simetria e a origem das vibrações

A causa raiz de vibrações mais frequentemente encontrada em turbomáquinas é o desequilíbrio que foi introduzido inadvertidamente, por exemplo, no conjunto do rotor da turbina-gerador.

O ponto fundamental a reconhecer é que a inércia de cada objeto gerara uma força que tenderá a colocar o rotor a girar em torno do seu verdadeiro centro de massa quando da aplicação de qualquer binário. Isto é provocado pela inércia das partículas que compõem o objeto ao iniciar o movimento circular induzido por um binário. A única forma de evitar esta rotação natural do centro de massa, é através de uma força de restrição que seja imposta ao objeto, para o manter em rotação não-centrada forçada, o que obriga o verdadeiro centro de massa a transladar-se lateralmente ou girar em torno do eixo de rotação forçado.

Como resultado desta imposta assimetria de rotação, uma parte da energia total fornecida pelo binário de entrada para acelerar a massa do rotor é convertida naquilo que é finalmente observado como “vibração” (mais precisamente, a deflexão radial e a translação lateral do veio no moente do rotor).

Esta energia manifesta-se na força centrífuga gerada pela inércia de qualquer porção de massa em rotação que, seja assimétrica em relação ao eixo de rotação forçada. Esta força é o que é tipicamente reconhecido como “desequilíbrio”. Em combinação com toda a força centrífuga está a(s) força(s) de reação do(s) ponto(s) de restrição que mantém esta forma forçada de rotação.

No que diz respeito à vibração do rotor do gerador de uma turbina, a grande maioria dos problemas de vibração surge quando a posição e orientação pretendida do rotor (centrada concentricamente em torno dos suas chumaceiras e acoplamentos) não corresponde ao local para onde o rotor quer naturalmente ir quando é acelerado pelo binário, dada a presença de excentricidade de massa (inerente a um rotor ou induzida por desalinhamento com outros rotores).

A quantidade de força parasita (ou potência, quando considerada ao longo do tempo) que atua para impulsionar a vibração do rotor está diretamente relacionada com a quantidade de força necessária para manter o rotor na sua posição de funcionamento pretendida quando este não tende naturalmente a fazê-lo.

Quando a excentricidade da massa está presente, os constrangimentos físicos que mantêm um rotor giratório horizontal no seu estado pretendido, mas “não natural”, são os moentes mantidos pela gravidade e os acoplamentos (e a massa ligada) dos rotores adjacentes.

A potência perdida nestas restrições é “roubada” da energia do binário de entrada e convertida em pontos de dissipação indesejados, nomeadamente material, vibração das estruturas de suporte, e em energia potencial que deflecte/dobra a “mola” do rotor à medida que o seu eixo de massa média se desloca lateralmente (gira) em torno do eixo do moente, particularmente, na primeira região de velocidade crítica.

É importante notar que, o objetivo da redução da vibração do rotor, deve centrar-se em restaurar a tendência natural de rotação (em torno do eixo do centro de massa) para coincidir com o eixo de rotação geométrico concêntrico projetado, centrado nos acoplamentos do rotor, para criar o comportamento dinâmico natural de um rotor idealmente concêntrico.

Ao fazê-lo, a maioria dos outros problemas dinâmicos (respostas ressonantes do rotor, instabilidades das chumaceiras, etc.) também desaparecem, uma vez que deixam de ter uma força motriz.

Na perspetiva da dinâmica de rotores mais tradicional, o pressuposto natural é que, abaixo da primeira velocidade critica, um rotor está sempre a rodar em torno do eixo geométrico, coincidente com o eixo dos moentes, a qualquer velocidade e qualquer assimetria de massa que cria vibração deve ser considerada como desequilíbrio em relação a este eixo de rotação. Assim, é comum a maioria das amplitudes de deslocação excessiva serem consideradas como alvos a serem resolvidos com forças de pesos de equilíbrio.

Isto pode criar problemas quando a quando a fonte real de assimetria de massa num rotor contínuo ou num conjunto de rotores provém de desalinhamento e empenos de rotor, ou quando a resposta de vibração indesejada está a ser observada acima da primeira velocidade crítica do sistema. Além disso, a colocação de pesos não permite necessariamente alcançar um verdadeiro estado “equilibrado”, definido como a soma de todas as forças e a soma de todos os momentos, sendo zero.

Quando não é alcançada uma verdadeira condição de equilíbrio, os momentos axiais residuais atuam para empenar ou distorcer o rotor, criam movimento e forças residuais e, frequentemente, criam uma orientação de auto-alinhamento “natural” modificada (dentro das folgas das chumaceiras e vedantes) que ainda não corresponde ao eixo geométrico do moente do rotor. Estas condições do rotor são identificáveis nos gráficos de vibração.

Turbomáquinas e Bodé – O significado físico das vibrações relativas e absolutas

As vibrações relativas medidas por um par de sensores de deslocamento indicam:

• O movimento relativo do veio relativamente às chumaceiras;
• O movimento do centro do veio.

As vibrações absolutas, medidas nas chumaceiras, indicam as forças transmitidas pelo veio às chumaceiras.

Turbomáquinas e Bodé – Os diferentes fatores que influenciam a amplitude e fase do Bodé

O deslocamento que se vê num gráfico de Bodé vai ser sempre ver o resultado de diversos efeitos, como por exemplo:

• Deslocamento devido à deformação associada aos modos de vibração quando se encontra próximo e acima das velocidades críticas;
• Deslocamento devido deformação associada a empenos e desalinhamentos;
• Deslocamento devido a desequilíbrio;
• Deslocamento devido à oscilação do moente do veio na pelicula de óleo.

Para perceber os gráficos tem de se entender como estes efeitos interagem.

Turbomáquinas e Bodé – A situação ideal

À medida que um grupo de rotores flexíveis aumenta de velocidade, a taxa de aumento da amplitude da deflexão radial, em conjunto com a mudança do ângulo de fase, indica quanto da amplitude de vibração observada é devida a um empeno estático e quanto é deflexão elástica induzida adicionalmente ou da associada respetivo modo de vibração.

No caso ideal, a amplitude deve permanecer plana ou com uma resposta muito pequena ao longo de toda a gama de velocidades e passando por uma variação do ângulo de fase em quaisquer velocidades críticas conforme se vê nos gráficos a seguir.

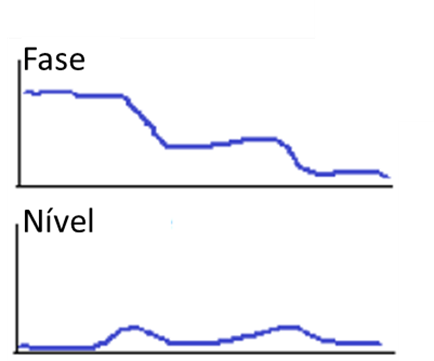
Turbomáquinas e Bodé – Figura 16

Turbomáquinas e Bodé – O desequilíbrio

Num gráfico de Bodé, o identificador mais importante da presença de desequilíbrio é o padrão de inclinação da amplitude em proporção à velocidade, em combinação com a presença ou ausência de deslocação do ângulo de fase radial.

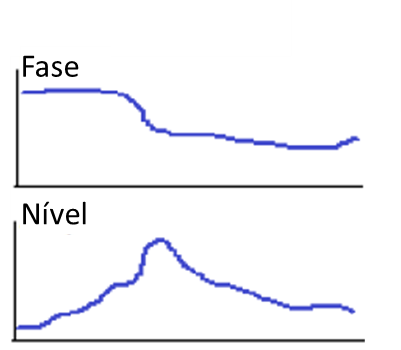
Turbomáquinas e Bodé – Figura 17

Turbomáquinas e Bodé – Run out e empeno e desalinhamento

Se a amplitude a baixa velocidade for já for diferente de zero, isto é indicativo de um empeno do rotor ou de desequilíbrio, e é também frequentemente proporcional à rigidez do rotor.

Uma amplitude diferente de zero a partir de uma velocidade baixa e permanecendo plana, e sem qualquer deslocação do ângulo de fase, sugere a presença de algum run-out ou de um empeno, ou a existência de um possível “efeito de manivela”, no conjunto dos rotores devido a um moente excêntrico ou a um acoplamento não-concêntrico conforme se vê nos gráficos a seguir.

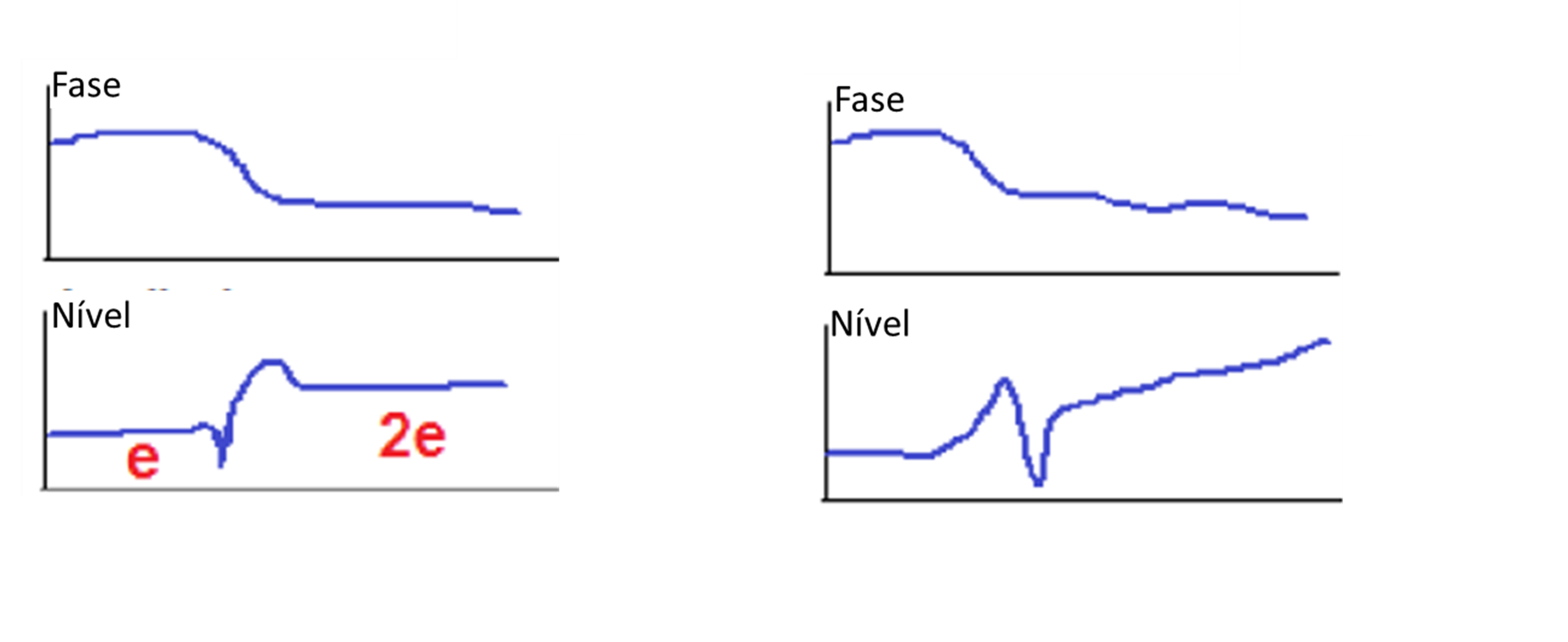
Turbomáquinas e Bodé – Figura 18

Um aumento inicial na amplitude sem mudança notável na fase sugere um empeno de rotor puro ou desequilíbrio que está a ser levada pela força centrífuga, a uma órbita do veio na chumaceira, de amplitude crescente, abaixo do início da primeira região de velocidade crítica conforme se vê nos gráficos a seguir.

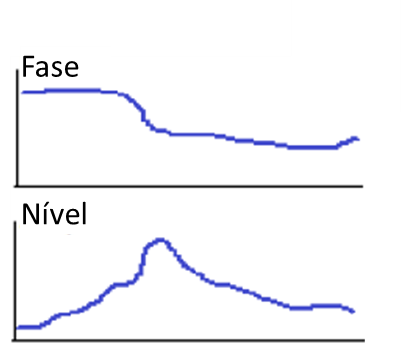
Turbomáquinas e Bodé – Figura 19

Esta é a condição em que o rotor está a ser forçado a percorrer um movimento, não concêntrico, com o seu eixo geométrico.

Se a amplitude continuar a aumentar enquanto o ângulo de fase começa a mudar, isso indica que está a ser adicionada uma componente dinâmica/forma de vibração ao movimento giratório conforme se vê no gráfico a seguir. Se a deslocação total do ângulo de fase for notavelmente inferior a 180 graus, isto indica que a amplitude da órbita do veio na chumaceira é dominante sobre qualquer deflexão elástica associada respetivo modo de vibração.

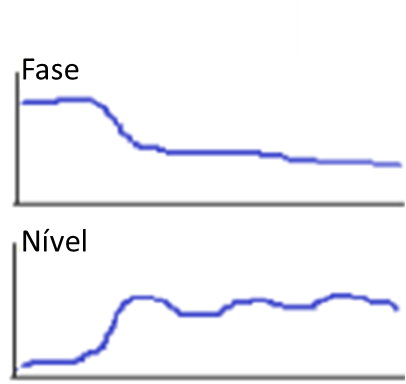
Turbomáquinas e Bodé – Figura 20

Turbomáquinas e Bodé – A influência do comportamento de outros rotores acoplados

Se o ângulo de fase se deslocar 180 graus, com uma alteração mínima na amplitude da deslocação, isso sugere que o rotor movimentado por um rotor vizinho, que passa pela sua região de velocidade crítica conforme se vê nos gráficos a seguir.

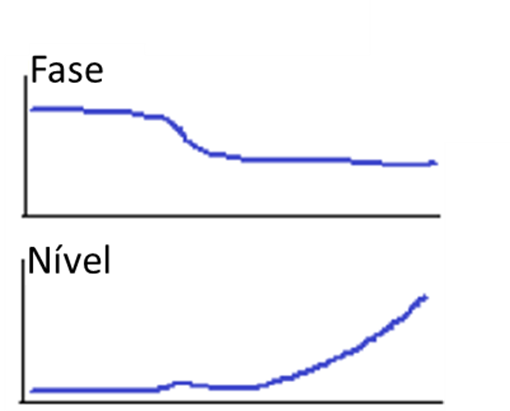
Turbomáquinas e Bodé – Figura 21

Da mesma forma, uma “saliência” do gráfico de Bodé na amplitude do deslocamento sem uma mudança de fase também pode vir da resposta de um rotor vizinho.

Tais situações são prontamente avaliadas através da revisão da gama de velocidades específica das respostas de amplitude e fase nos gráficos de Bodé de todos os rotores.

Em casos como este, é muito dispor de um modela de Elementos Finitos dos rotores para identificar as frequências naturais inerentes de cada rotor.

Turbomáquinas e Bodé – Movimento de oscilação do rotor – assimetria axial na distribuição da excentricidade

A velocidades acima da primeira velocidade crítica, uma tendência de amplitude ascendente sem qualquer mudança notável do ângulo de fase é uma indicação imediata de assimetria axial na distribuição da excentricidade que gera o modo de oscilação/pivotagem conforme se vê nos gráficos a seguir.

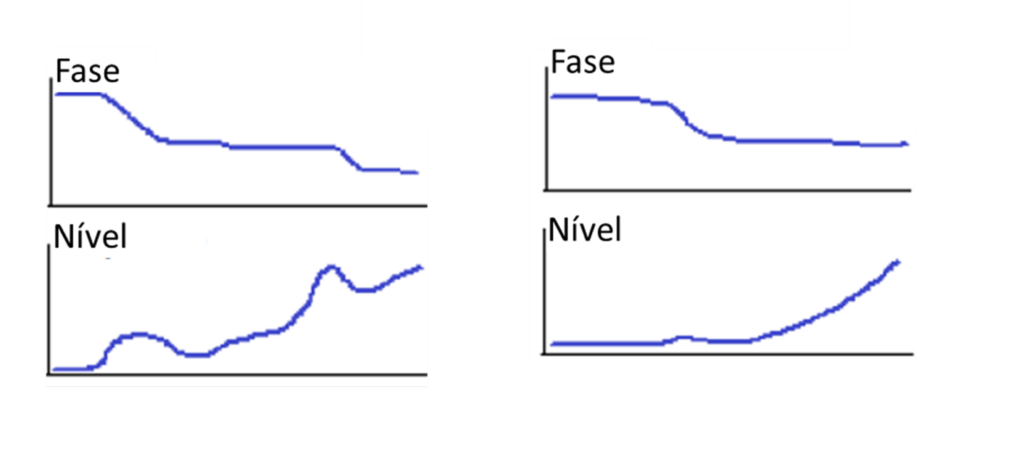
Turbomáquinas e Bodé – Figura 22

Por vezes, observa-se uma resposta de amplitude adicional com uma deslocação do ângulo de fase sobreposta à tendência ascendente que é indicativa de uma resposta ressonante na segunda velocidade crítica, conforme se vê no gráfico anterior (lado direito).

Turbomáquinas e Bodé – Excentricidade

Outra indicação comum de excentricidade é quando a amplitude acima da primeira velocidade crítica é aproximadamente o dobro da medida abaixo da primeira velocidade crítica, ou simplesmente permanece elevada, mas algo plana conforme se vê nos gráficos a seguir.

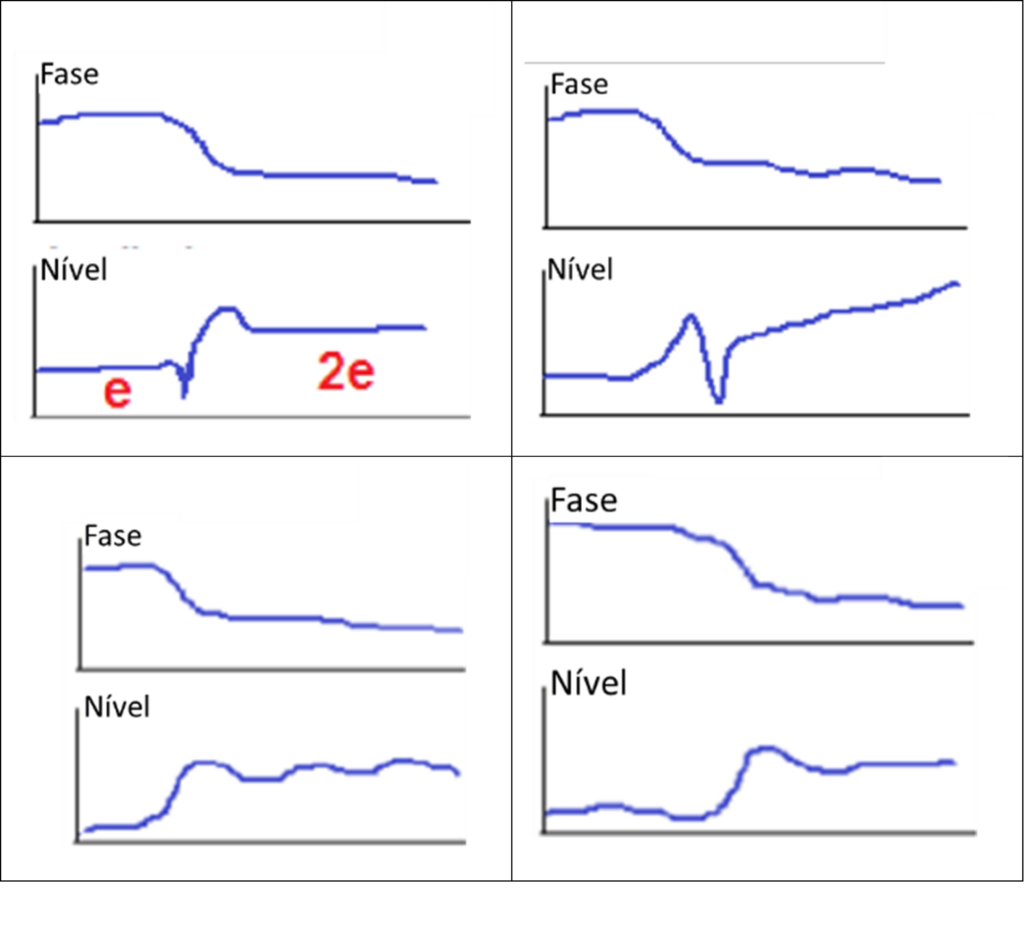
Turbomáquinas e Bodé – Figura 23

Isto é uma função do rotor que muda a posição do seu eixo de rotação quando passa pela região de velocidade crítica. A velocidades mais baixas, os sensores medem a quantidade direta de excentricidade do eixo da massa em rotação em torno do eixo do geométrico, indicando uma amplitude igual à excentricidade, e. Quando o rotor é suficientemente flexível, pode ser medida uma amplitude reduzida no moente, uma vez que o rotor pode principalmente “oscilar” ou fletir no seu plano médio, absorvendo a maior parte da força correspondente.

A velocidades mais elevadas, os sensores vêm o “rotor inteiro” a girar em torno do eixo de inercia enquanto continua a rodar, de tal forma que os sensores medem a excentricidade intrínseca, bem como a medida da excentricidade, indicando uma amplitude de 2e.

Turbomáquinas e Bodé – Reduções de amplitude devido à mudança de posição do eixo de rotação

Por vezes, também se observa uma breve descida da amplitude antes ou depois do pico de velocidade crítica. Esta queda corresponde a um breve momento de auto-equilíbrio do rotor na transição entre eixos de rotação. Se for antes do crítico, indica que a resposta ressonante é dominante, e se for visto após o crítico, indica que o modo rígido impulsionado pela excentricidade e força centrífuga é dominante conforme se vê nos gráficos a seguir.

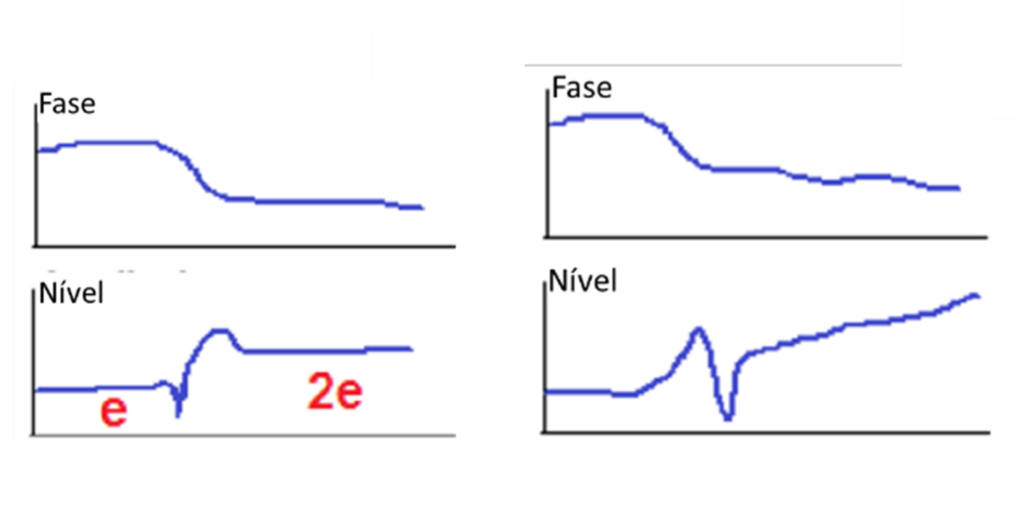
Turbomáquinas e Bodé – Figura 24