Isolamento de vibrações

Neste artigo trata-se do tema do isolamento de vibrações e regras de suas montagem, revendo-se o tema dos sistemas com um grau de liberdade.

1 –        DESCRIÇÃO DE UM SISTEMA DINÂMICO SIMPLES

1.1 –     Introdução

Os sistemas que a seguir se vão descrever são os seguintes:

            – Movimento livre com um grau de liberdade, não amortecido

            – Movimento livre com um grau de liberdade, amortecido

            – Movimento forçado com um grau de liberdade, não amortecido

            – Movimento forçado com um grau de liberdade, amortecido

Na verdade, todos os sistemas físicos dispõem de uma infinidade de graus de liberdade. Todavia uma análise preliminar evidenciará que algumas componentes do movimento são, ou desprezáveis ou sem interesse podendo desde logo ser suprimidas para efeitos de estudo do fenómeno que se quer observar. Assim reduzem-se o número de graus de liberdade a estudar.

1.2 –     Conceitos Básicos

Uma máquina pode ser representada como um sistema de massas m_i, ligadas entre elas por elementos de rigidez Ki, possuindo um amortecimento Ci.

Relembremos estas noções.

MASSA

Uma massa é um corpo rígido cuja aceleração, de acordo com a lei de Newton, é proporcional à resultante das forças que sobre ela atuam.

A unidade de massa é o Kg ou o Ns²/m.

RIGIDEZ

Consideremos uma mola linear:

A variação do comprimento da mola é proporcional á força nela aplicada.

                                                                   F= K (x-u)

Considera-se uma mola ideal sem massa. A força que atua de um lado é igual e oposta à força atuante do outro lado. A constante de proporcionalidade k é chamada de Rigidez da mola.

A unidade em que k se exprime é o N/m.

AMORTECIMENTO

Considere-se um sistema de amortecimento viscoso como o que a seguir se pode ver.

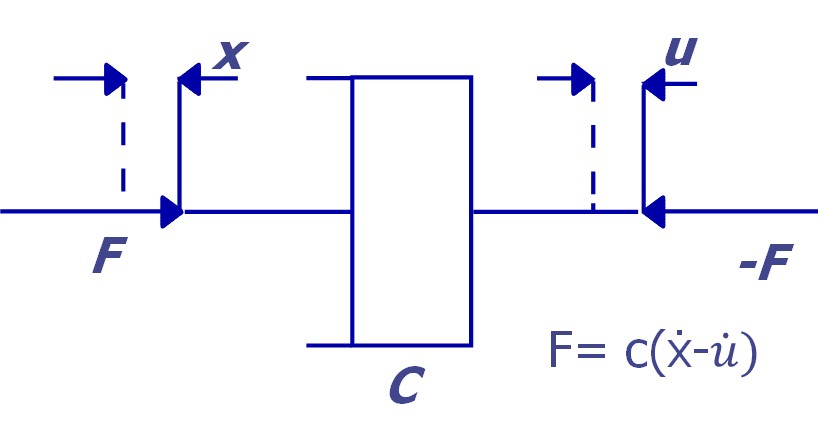
No amortecimento viscoso a força aplicada é proporcional à velocidade relativa do ponto de aplicação.

A unidade em que se exprime C é o Ns/m.

A constante C é o coeficiente de amortecimento, parâmetro característico de um amortecedor. Considera-se um amortecedor ideal sem massa. A força que atua de um lado é igual e oposta àquela que atua do centro.

As equações características podem-se assim escrever de um modo geral da seguinte forma:

Outras definições que convém ter presentes são as seguintes:

Movimento livre –	Movimento com ausência de força exterior
Movimento não amortecido –	Movimento sem qualquer efeito de amortecimento
Movimento com um grau de liberdade –	Movimento só numa direção

1.3 –     Movimento Livre não Amortecido com um Grau de Liberdade

Considere-se por exemplo um sistema constituído por uma massa M ligada a um ponto fixo por uma mola K. Considere-se também que a massa só se pode mover numa direção.

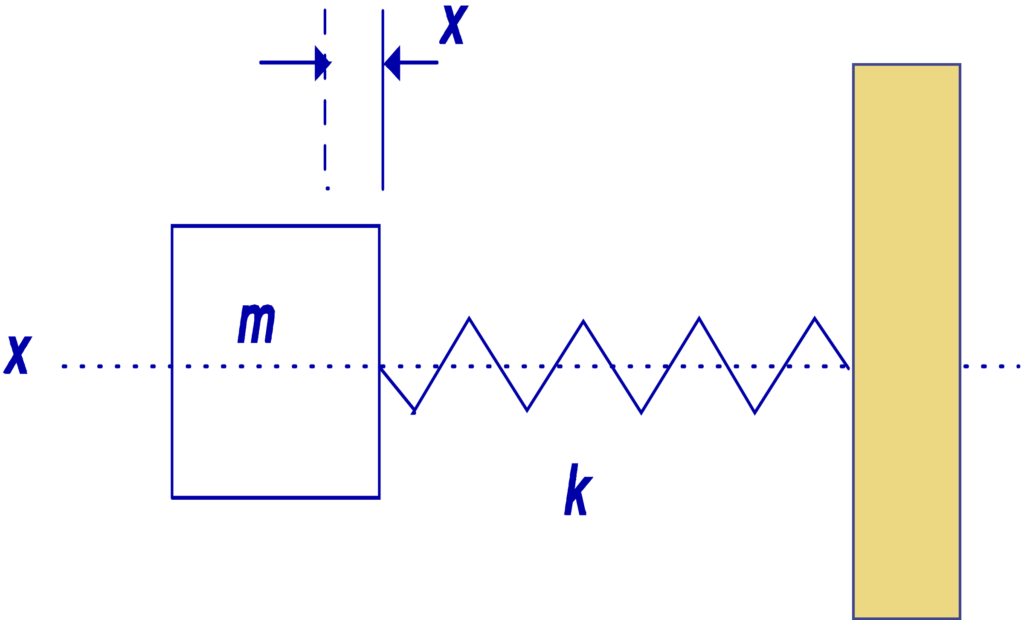
A equação que descreve o movimento da massa é:

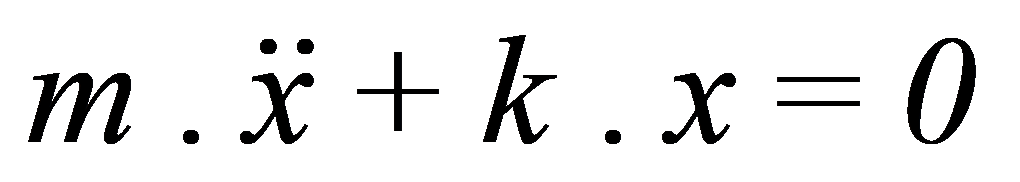
A solução desta equação é:

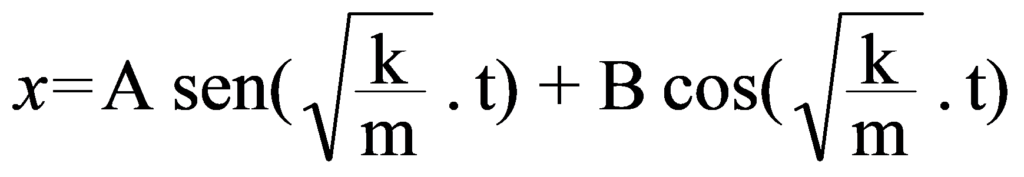
A e B são duas constantes que podem ser determinadas a partir das condições iniciais de velocidade e deslocamento quando t=0.

Este movimento é, portanto, do tipo sinusoidal cuja frequência é:

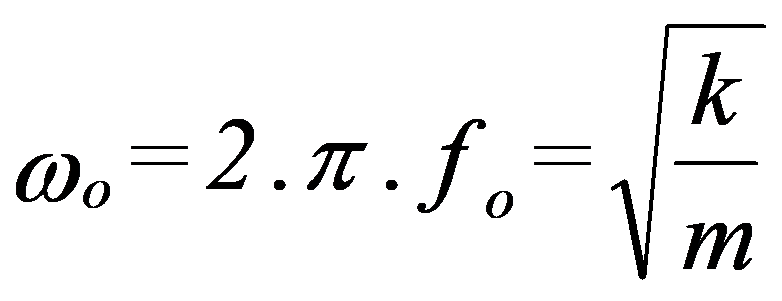
Esta frequência é chamada de Frequência Natural ou Frequência Própria do sistema.

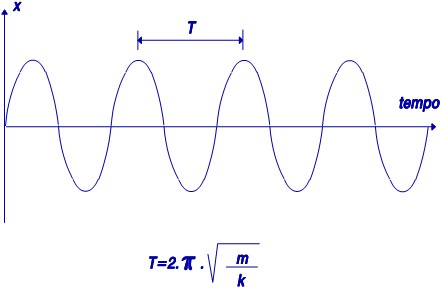
Não existindo amortecimento este sistema permanecerá em movimento indefinidamente como se pode ver na figura.

O exemplo das forças numa máquina rotativa

A causa de raiz de vibração excessiva, mais frequentemente encontrada em máquinas é a excentricidade de massa. A excentricidade de massa deve ser vista do ponto de vista da simetria do rotor, no que diz respeito ao reconhecimento do comportamento natural após a conservação do momento angular. O ponto fundamental a reconhecer é que cada objeto tenderá natural e livremente a girar sobre o seu verdadeiro centro de massa (ou eixo de inércia) após a aplicação de qualquer binário. Isto é impulsionado pela inércia das partículas que compõem o objeto ao iniciar o movimento circular de rotação. A única forma de impedir esta rotação em torno do centro de massa) é quando alguma forma de força de restrição é imposta ao objeto em rotação para o manter em alguma rotação forçada, não centrada, que força o verdadeiro centro de massa a traduzir lateralmente ou rodopiar em torno do eixo de rotação forçada.

Como resultado desta assimetria rotacional imposta, uma porção da energia total fornecida pelo binário de entrada para acelerar a massa do rotor é convertida naquilo que é finalmente observado como “vibração” (mais precisamente, a deflexão radial e a translação lateral do eixo do moente do rotor). Esta energia manifesta-se na força centrífuga gerada pela inércia de qualquer parte da massa em rotação que seja assimétrica, em relação ao eixo forçado de rotação/rotação. Esta força é o que é tipicamente reconhecido como “desequilíbrio” durante a rotação. Em combinação com toda a força centrífuga é a(s) força(s) de reação a partir do(s) ponto(s) de restrição, mantendo esta forma forçada de rotação.

1.4 –     Movimento Livre Amortecido com um Grau de Liberdade

O amortecimento é devido ao surgimento de forças passivas que se opõem às velocidades. O amortecimento viscoso, que é frequentemente encontrado, apresenta a grande vantagem de conservar a linearidade das equações; de facto as forças passivas são proporcionais à velocidade.

No caso de se juntar um amortecedor entre a massa e o ponto fixo, a equação característica do movimento, na ausência de forças exteriores, é a seguinte:

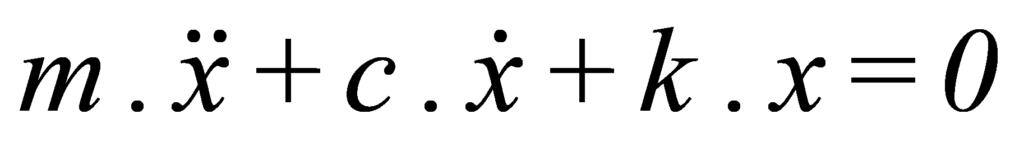
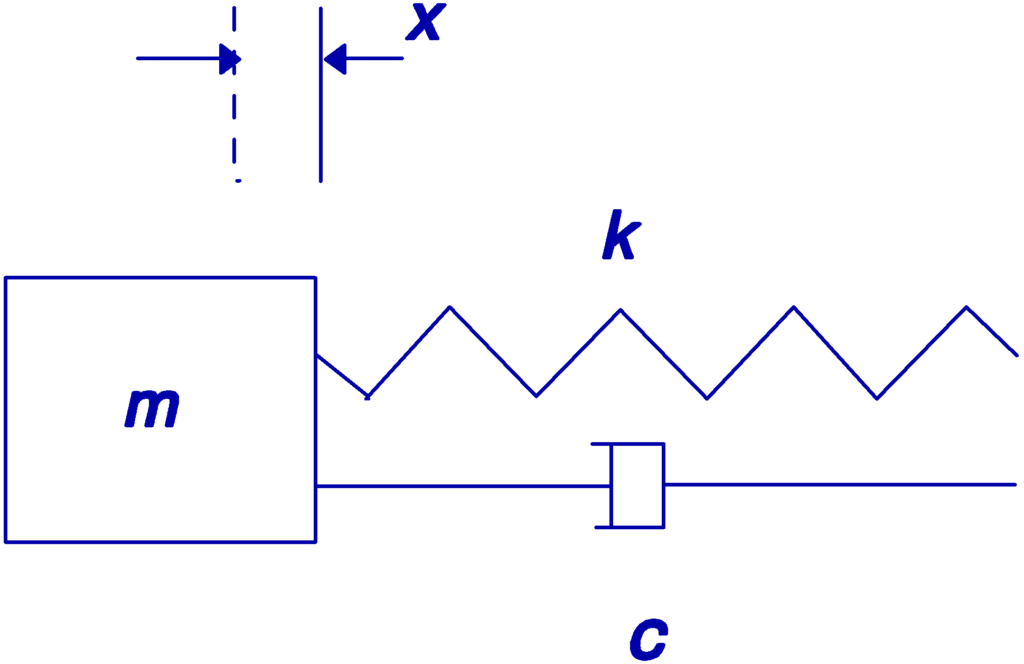
Define-se normalmente um coeficiente chamado de Coeficiente de Amortecimento Crítico e com o valor:

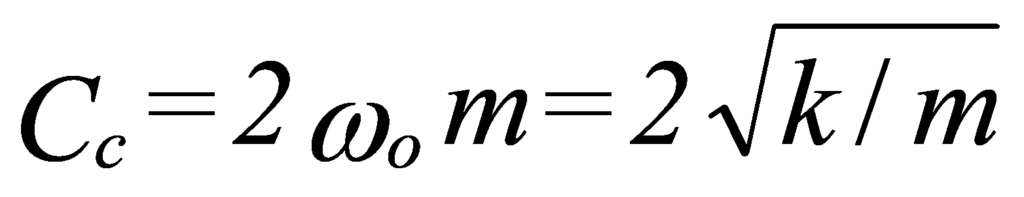
Segundo o valor de em relação a ξ, a equação a apresentará diversas soluções:     

       

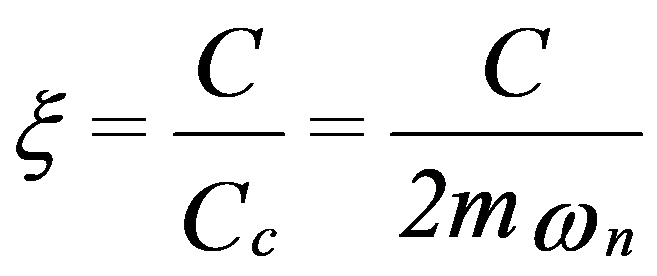
A)   ξ<1  – Movimento subamortecido

A solução da equação é dada por:

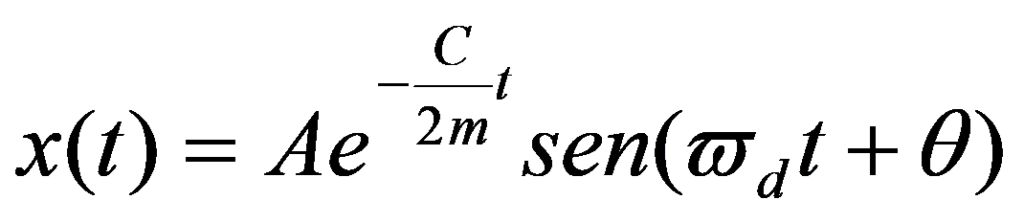
A = constante, função das condições iniciais

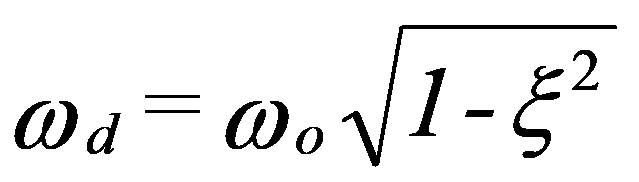
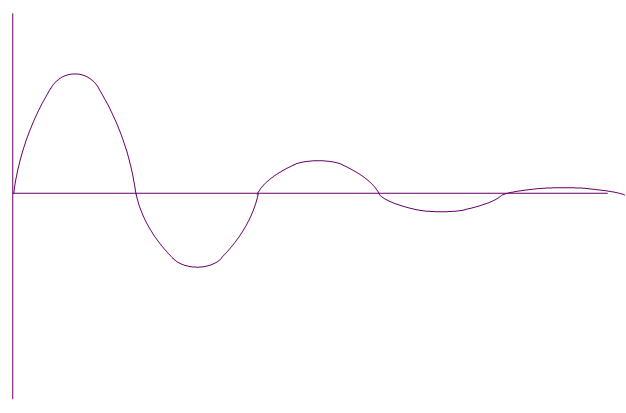
A evolução deste movimento pode ser vista na figura a seguir apresentada. Constata-se que o sistema tende a voltar para a sua posição de equilíbrio no seguimento de sucessivas oscilações. As oscilações são moduladas por uma exponencial decrescente.

B) ξ=1 C=C_c (amortecimento crítico)

Não ocorrem oscilações e o sistema tende para a sua posição de equilíbrio de acordo com a seguinte equação:

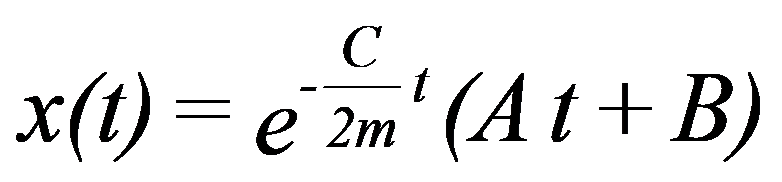
A e B são constantes que dependem das condições iniciais.

C) ξ>1 C>C_c    Movimento Sobre-amortecido   

O movimento é igualmente não oscilatório e é descrito pela seguinte equação:

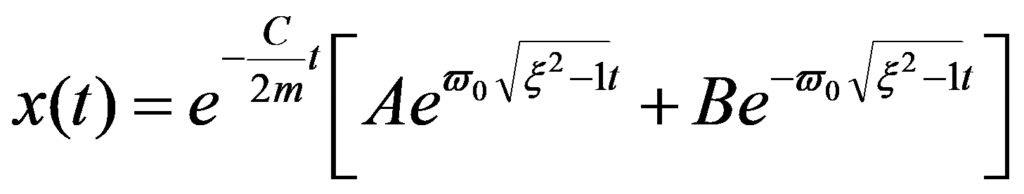
1.5 –     Movimento forçado com um grau de liberdade não amortecido e isolamento de vibrações

Um caso muito importante ocorre quando se aplica a um sistema uma força periódica.

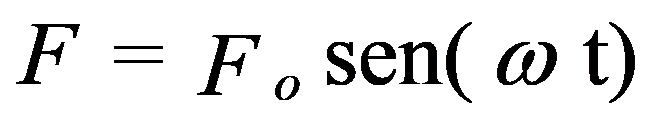
Este sistema pode por exemplo representar uma máquina de massa m ligada ao solo por uma estrutura com rigidez k.

A força F pode ser, por exemplo, originada por um desequilíbrio no rotor da máquina que roda à velocidade de rotação.

A equação característica deste sistema pode ser escrita da seguinte forma:

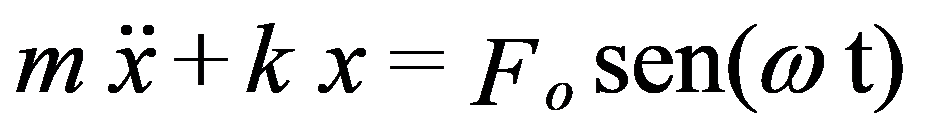
em que  é a velocidade angular da força excitadora.

A solução desta equação assume a seguinte forma:

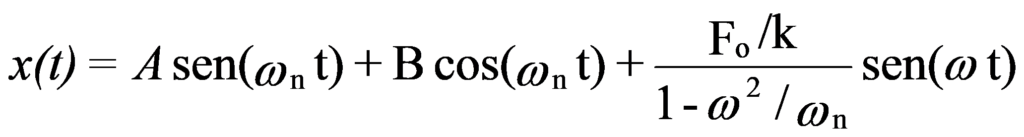
A e B são constantes função das condições iniciais.

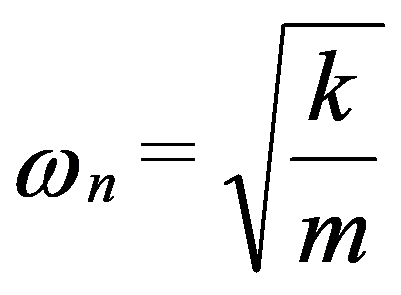
Os dois primeiros termos representam uma oscilação à Frequência Própria ω_n, exatamente do mesmo modo que foi determinado para o movimento livre não amortecido. Já se viu que por efeito do amortecimento esta oscilação desaparece ao fim de algum tempo. Restará, portanto, como única solução estável uma vibração forçada à frequência ω cuja amplitude será:

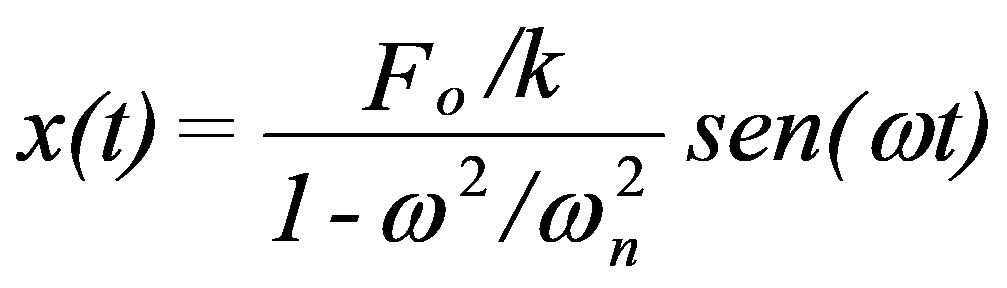
A seguir pode-se ver uma demonstração sobre a influência da massa, na frequência natural, de um sistema com um grau de liberdade.

1.6 –     Movimento Forçado com um Grau de Liberdade com Amortecimento

Considere-se um sistema semelhante ao precedente, mas agora com um dispositivo amortecedor.

Pode-se de novo escrever a equação característica deste sistema:

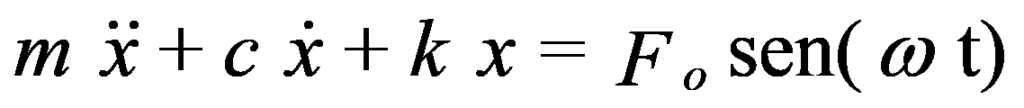
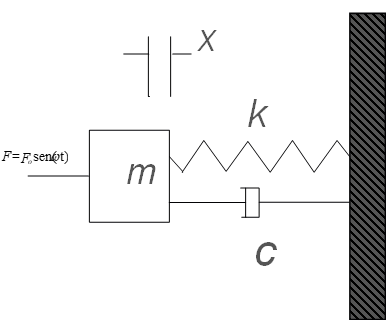
Quando o amortecimento é diferente de zero (C≠0), o deslocamento x pode ser descrito aproximadamente pelas seguintes fórmulas:

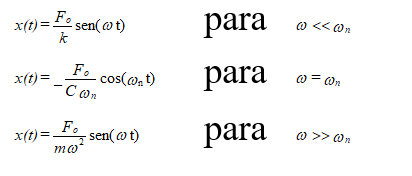
Estas são as soluções estáveis, não entrando, portanto, em conta com as oscilações à frequência própria do sistema que desaparecem ao fim de algumas oscilações.

Constata-se que, quando a frequência da força excitadora ω é igual à frequência própria do sistema (segundo caso), a amplitude é inversamente proporcional ao amortecimento. No caso dum fraco amortecimento, pode ser perigoso operar uma máquina a uma velocidade próxima da frequência própria do sistema (normalmente designada por velocidade crítica da máquina) devido ao facto dos níveis das vibrações poderem assumir valores muito elevados.

A relação entre a resposta resultante em amplitude x, e o deslocamento que o sistema sofreria se a força f fosse aplicada estaticamente x_st =f/k chama-se Fator de Amplificação Q:

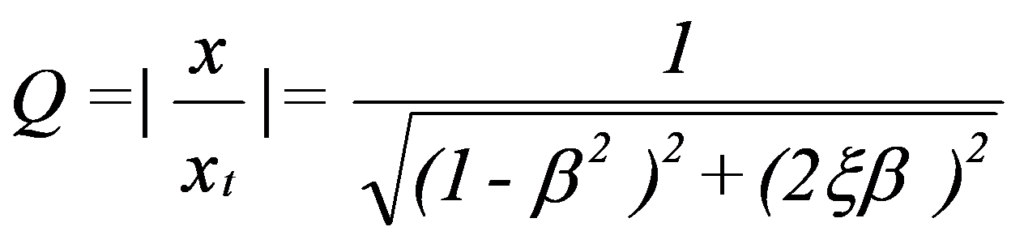
em que se tem:

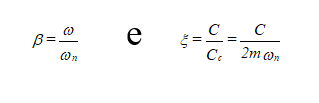
Na figura pode-se ver a apresentação gráfica desta equação.

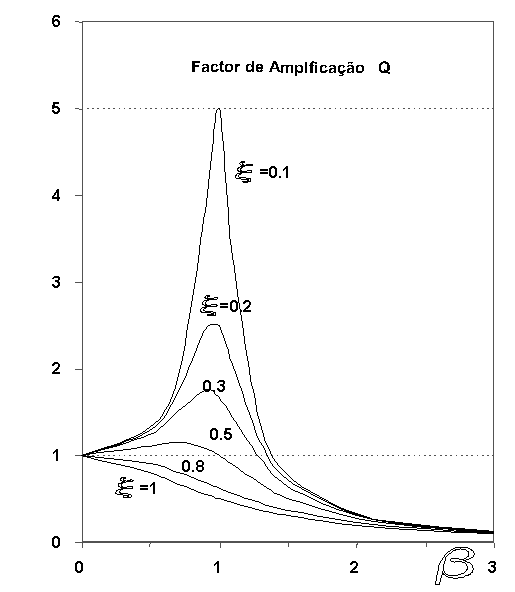
A seguir pode-se ver uma demonstração sobre a relação entre a força excitadora e a amplitude do movimento, a diversas frequências, num sistema com um grau de liberdade.

2 –        O ISOLAMENTO DAS VIBRAÇÕES

2.1 –     A Escolha dos Apoios no isolamento de vibrações

No caso do isolamento das vibrações, o parâmetro que interessa considerar é o relativo à força transmitida á fundação ou base da máquina. Este parâmetro é a transmissibilidade T.

Este parâmetro exprime a relação existente entre a força transmitida à fundação Ft, e a força de excitação Fo.

A força transmitida à fundação pela mola e pelo amortecedor é:

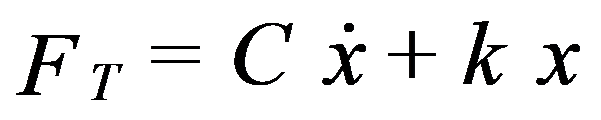
A Transmissibilidade é dada por:

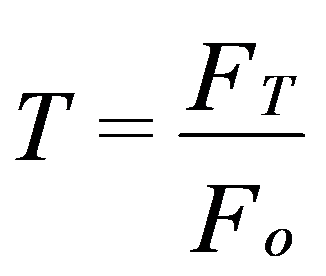
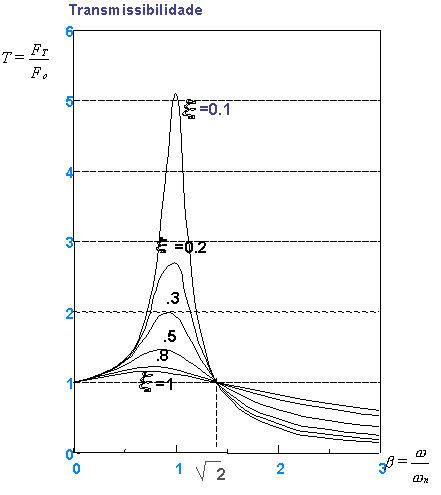
Quando a relação ω/ω_n =1 (frequência excitadora = frequência própria do sistema), ocorre o fenómeno de ressonância e a transmissibilidade é largamente superior a um. A amplitude da resposta do sistema F_T é assim superior à da excitação F₀; ocorre uma amplificação das vibrações.

Se o amortecimento do sistema for nulo, a amplitude da resposta quando ocorre ressonância, torna-se infinita.

Na prática o amortecimento C é regra geral inferior ao amortecimento critico C_c..

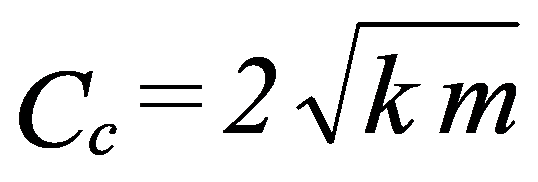
Note-se que quando ocorre ressonância, a amplitude diminui quando aumenta o amortecimento. Para uma relação ω/ω_n < √2, T é maior que um e o amortecimento tem uma função atenuadora.

Pelo contrário, quando ω/ω_n > √2, ocorre uma atenuação da transmissão da força, ou seja, quando a frequência própria do sistema é inferior à frequência forçada. Neste caso, todavia, o amortecimento tende a aumentar a transmissibilidade. Neste último caso não se deve concluir que o amortecimento se torna desinteressante; de facto o seu efeito não é muito grande para ω/ω_n > √2 , e pode ser compensado utilizando molas menos rígidas (ou seja, reduzindo ω_n). Para além disso, mesmo que não se pretenda operar a máquina em ressonância, podem ocorrer situações excecionais em que isso ocorra e torna-se indispensável a existência de amortecimento.

Assim as fundações podem ser isoladas de uma máquina intercalando entre elas um material elástico tal que a frequência própria da máquina sobre o seu suporte seja muito mais pequena (pelo menos três a quatro vezes) que a frequência fundamental da força periódica. Como é evidente as harmónicas serão tanto mais atenuadas quanto maior for a sua ordem, sobretudo se não existir um grande amortecimento.

Um parâmetro que se encontra frequentemente nos catálogos dos fornecedores de apoios anti vibratórios é a Redução de Força.

Redução de força (RF) = 1 – Transmissibilidade

Para se obter um adequado isolamento, a Frequência Natural ω_n deve ser baixa (β=ω/ω_{n >}1) e o Amortecimento C deve ser reduzido. Considerando-se assim o caso de amortecimento nulo a Transmissibilidade é:

A Redução de Força virá assim dada por:

Como se tem:

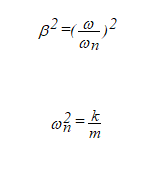
Sendo a deformação estática de uma mola:

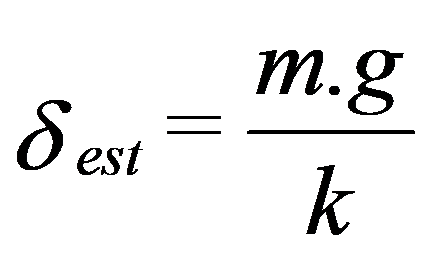
Tem-se que a Redução de Força será:

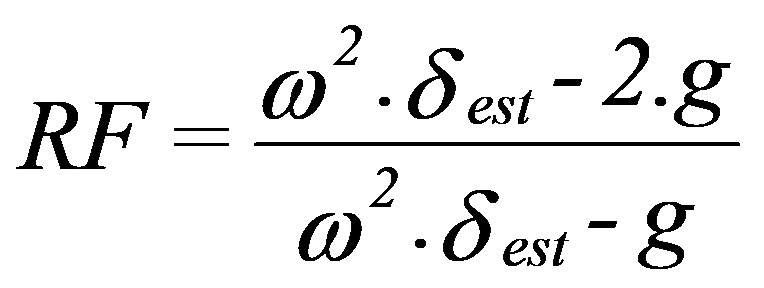
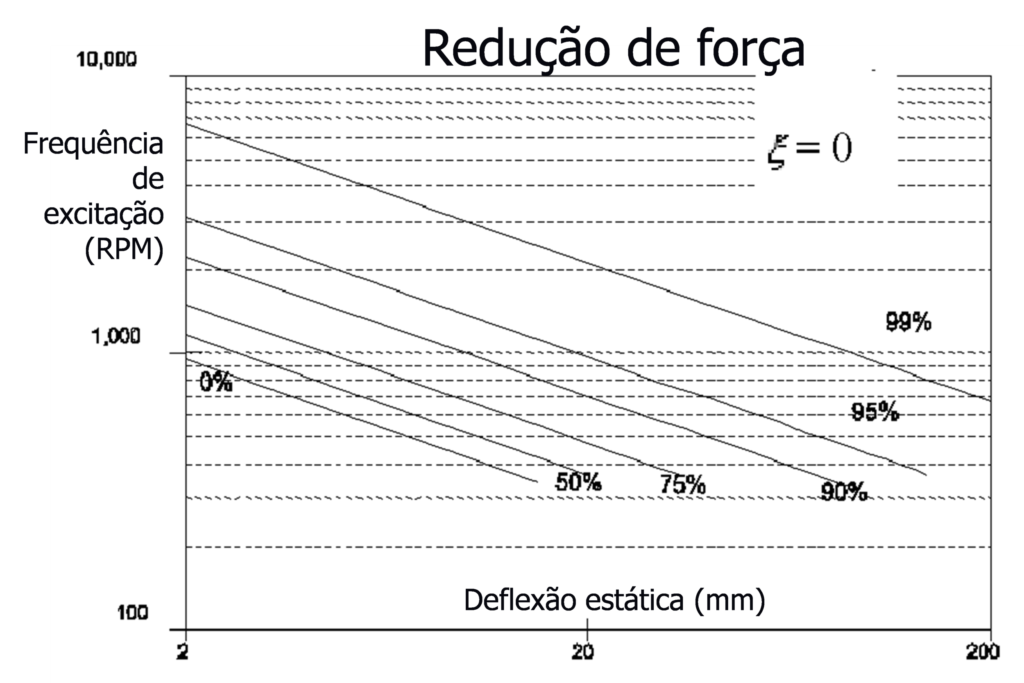
A figura a seguir apresentada mostra a representação desta equação.

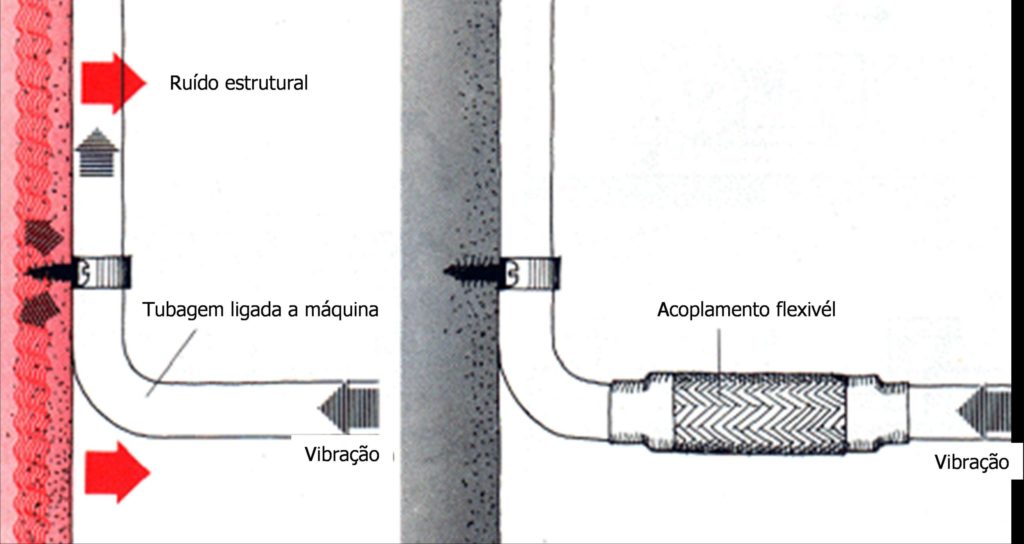
A eficiência de um isolamento pode ser significativamente reduzida se o sistema a isolar tiver ligações rígidas a estruturas vizinhas, como sejam por exemplo tubagens, perfis, etc. Qualquer ligação, deve ser tão flexível quanto possível, tanto para isolar as vibrações como para evitar que as ligações se danifiquem.

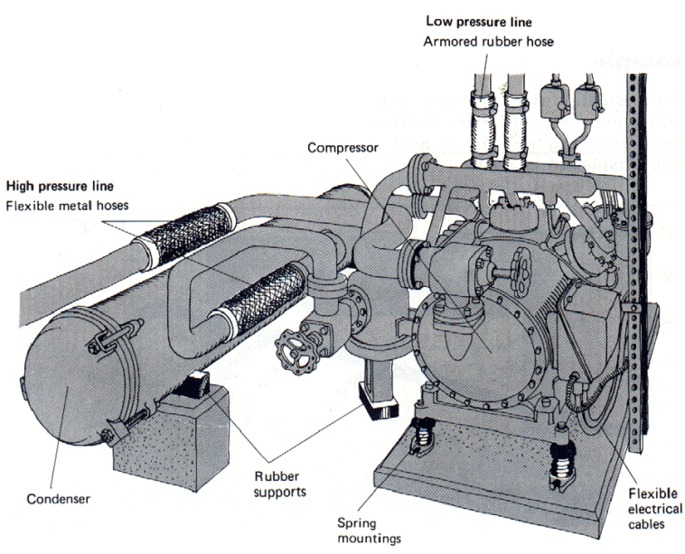
Este tipo de isolamento anti vibratório, em que se pretende que as vibrações geradas numa máquina não se propaguem á estrutura onde está apoiada designa-se de isolamento ativo.

Quando o isolamento tem por fim evitar que a vibrações ambientais atinjam uma determinada instalação designa-se então por isolamento passivo.

Algumas regras práticas:

–           Normalmente considera-se que um isolamento de 80 % das vibrações é suficiente

–           Tipicamente a frequência natural do sistema apoiado deverá ser 1/3 ou 1/4 da frequência mais baixa a isolar que normalmente é a velocidade de rotação.

–           Os apoios devem ser colocados nos vértices da base.

  –         Depois dos apoios serem instalados deve-se verificar que a deflexão estática é igual para todos.

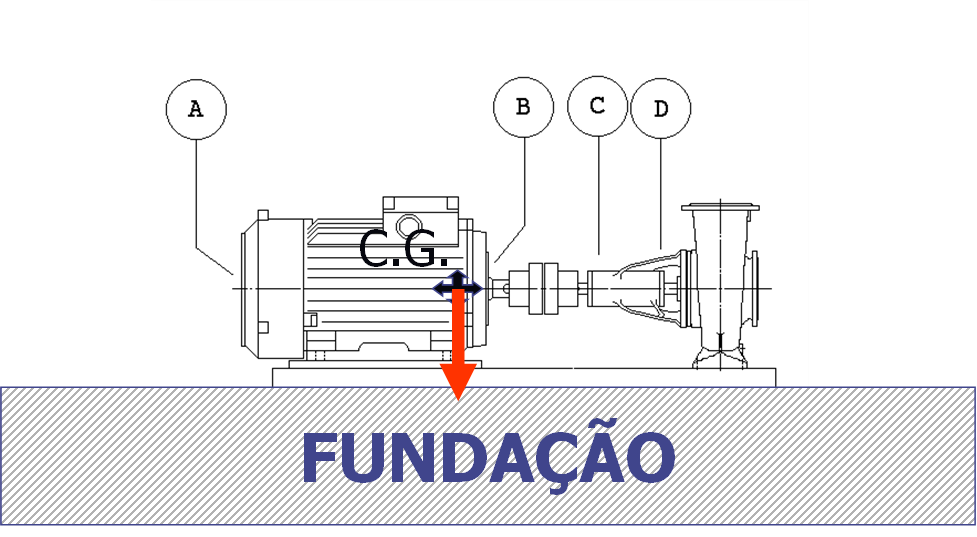
2.2 –     A Montagem – Posição dos Apoios em Relação ao Centro de Gravidade eo isolamento de vibrações

É extremamente importante que os apoios estejam corretamente colocados em relação ao centro de gravidade. Na maioria dos casos todos os apoios são semelhantes e são excitados de igual forma em amplitude e frequência; assim estão adequadamente instalados quando tiverem uma deflexão igual em todos eles. É assim muito importante que os apoios estejam distribuídos simetricamente em relação ao centro de gravidade e aos principais eixos de inércia. O não cumprimento desta regra pode levar a que a uma excitação na direção vertical, correspondam movimentos nas outras direções.

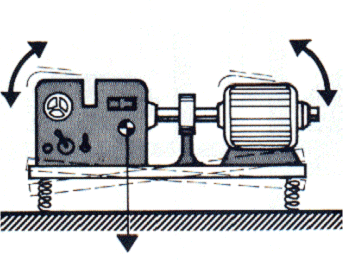
Ocorrem, no entanto, casos em que isto não se verifica e, portanto, tem de se entrar com isso em conta.

1º Caso – Apoios ligados a pontos fixos da máquina

A rigidez dos apoios tem de ser ajustada.

            P                      –  Carga total

            P1,P2               –  Carga nos apoios P1 e P2

            K1,K2             –  Rigidez dos apoios 1 e 2

                 delta                    –  Deflexão estática

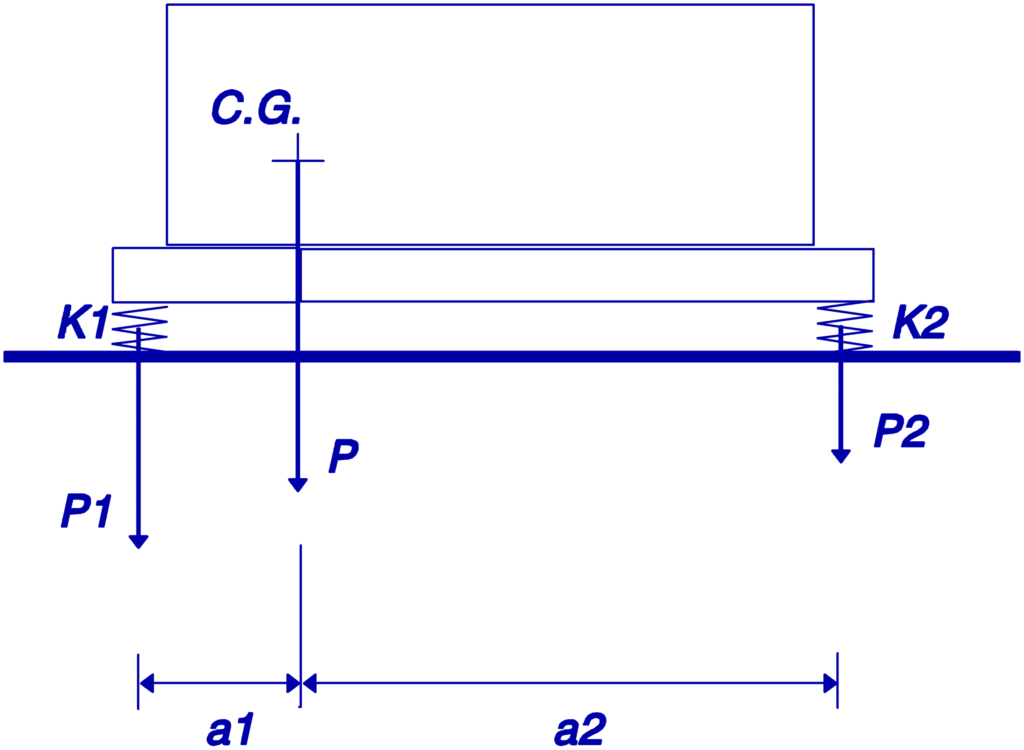
A condição de equilíbrio é:

a1×P1=a2×P2

Então tem-se:

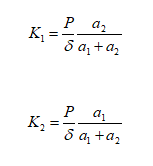
Ter-se-á então que escolher apoios com uma rigidez tão próxima quanto possível de K1 e K2.

2º Caso – É possível escolher a posição de colocação dos apoios

Utilizam-se apoios idênticos e colocam-se assimetricamente de modo a receberem cargas iguais.

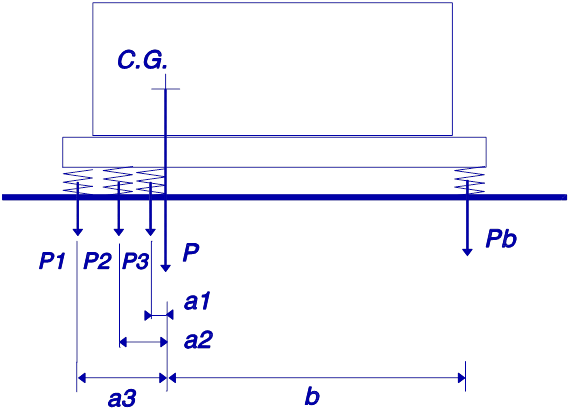
Condição de equilíbrio:

Condição de equilíbrio:

∑ (a_i. P_i) = ∑ (b_j.P_j)

Se todos os apoios forem iguais devem ser colocados de modo a ∑a_i=∑b_j.

Estas fórmulas assumem que a estrutura assente nos apoios anti vibratórios é rígida. Caso a estrutura não seja rígida a condição de equilíbrio poderá ser encontrada experimentalmente.

Neste link pode-se ver um exemplo dos efeitos de uma avaria num isolamento de vibrações.

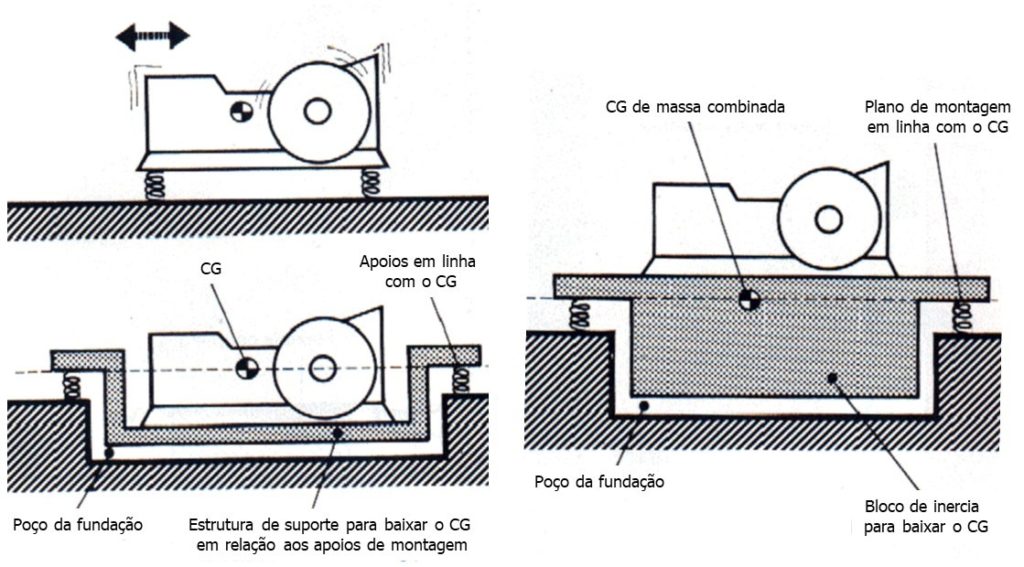
2.3 –     O Bloco de Inércia e o isolamento de vibrações

O isolamento das vibrações é obtido pela frequência natural e amortecimento do sistema de apoio. Assim a função do bloco de inércia não é isolar as vibrações.

O bloco de inércia tem diversas funções:

– Reduzir a amplitude do deslocamento devido às vibrações aumentando a relação entre a massa estática e as forças dinâmicas. É, portanto, utilizado quando as forças dinâmicas são grandes ou se quer reduzir o deslocamento.

– Baixar o centro de gravidade para se obter um melhor equilíbrio do sistema em caso de distribuição assimétrica de massas.

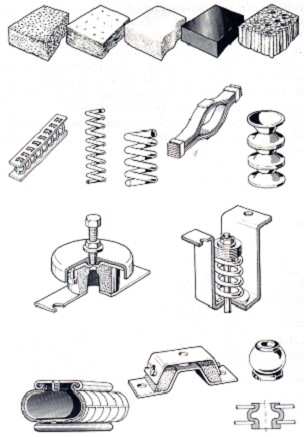
2.4 –     Materiais Usados em apoios anti vibratórios

Existem muitos materiais usados em apoios anti vibratórios para isolamento de vibrações. Aqui vai-se apenas falar de alguns.

Cortiça

A cortiça utiliza-se tanto à compressão como ao corte. As suas propriedades dependem da frequência e da carga a que está submetida. Para maiores cargas torna-se mais flexível.

Molas

As molas são os elementos elásticos que permitem maiores deflexões estáticas, e em que, portanto, se conseguem atingir frequências mais baixas. Têm, contudo, muito pouco amortecimento apresentando também deslocamentos importantes. Suportam condições ambientais muito agressivas.

Borracha

A maioria dos apoios em borracha trabalha ao corte para maior flexibilidade. As suas propriedades variam muito com a temperatura e frequência. Degradam-se na presença de óleo e gasolina.

Elastómetros Sintéticos

Os elastómetros têm a vantagem de poder suportar forças à tração, à compressão e ao corte. No entanto só com dificuldade se obtêm montagens com frequências inferiores a 5 Hz.

3 –        O AMORTECIMENTO DAS VIBRAÇÕES E O ISOLAMENTO DE VIBRAÇÕES

As estruturas exibem teoricamente um número infinito de ressonâncias. Se forem submetidas a excitações de frequência variável ou a uma larga banda de frequência de vibrações aleatórias podem ser excitadas sempre um certo número de ressonâncias. Devido ao facto da maioria dos materiais utilizados em engenharia, como sejam por exemplo os casos do alumínio e o aço, apresentarem muito pouco amortecimento interno, torna-se necessário reduzir os efeitos das ressonâncias com uma ação externa. No caso das chapas utiliza-se por vezes uma rigidificação. No entanto este tipo de efeito não amortece as ressonâncias; transfere-as sim para uma frequência superior. Caso as frequências de ressonância possam ser transferidas para uma zona onde não sejam excitadas durante a utilização normal dos equipamentos, esta solução pode ser aceitável.

Por outro lado, em estruturas complexas a transferência de ressonâncias para outras frequências pode originar consequências nefastas nalgumas componentes. Tem-se assim que a solução mais geral para este tipo de problemas consiste em aplicar algum tipo de amortecimento externo aos materiais.

O amortecimento externo pode ser aplicado de diversas maneiras:

a)         Por meio de amortecimento gerado no atrito de superfícies

b)         Através da aplicação superficial de um material com grande amortecimento

c)         Utilização de estruturas em sanduíche

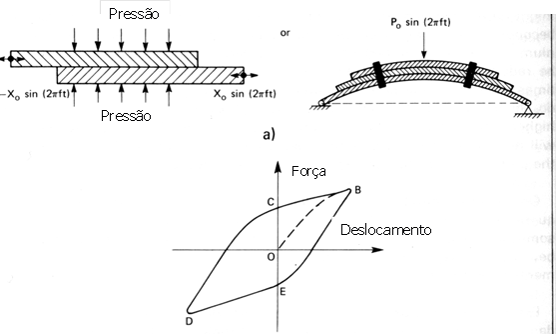
3.1 –     O Amortecimento por Atrito

O amortecimento de atrito é obtido permitindo que duas superfícies deslizem uma sobre a outra conforme se pode ver na Figura. Se não existir lubrificante entre as duas superfícies o efeito de amortecimento é provocado pelo atrito seco. A relação entre a força e o deslocamento, para este tipo de amortecimento, é apresentada na Fig.22. A energia vibratória deste modo dissipada é dada pela área dentro da curva B-C-D-E-B. Este tipo de amortecimento é usado nas molas de barras.

3.2 –     Aplicação de Materiais Amortecedores

Uma das maneiras mais simples de introduzir amortecimento numa componente de uma estrutura a vibrar consiste na aplicação de uma camada de um material viscoelástico, com perdas internas importantes, na superfície da componente. Este tipo de técnica de amortecimento é largamente utilizado na indústria automóvel há muitos anos. O material mais conhecido para este fim é o chamado mastic, feitos a partir de asfalto.

Este tipo de materiais, são constituídos por polímeros, e têm propriedades ótimas numa determinada gama de frequência e temperatura.

Para se obter o melhor amortecimento do conjunto componente estrutural + material amortecedor, o fator de perda interna e o módulo de elasticidade do material amortecedor devem ser elevados.

A fórmula aproximada a seguir apresentada descreve as características de amortecimento de uma superfície tratada:

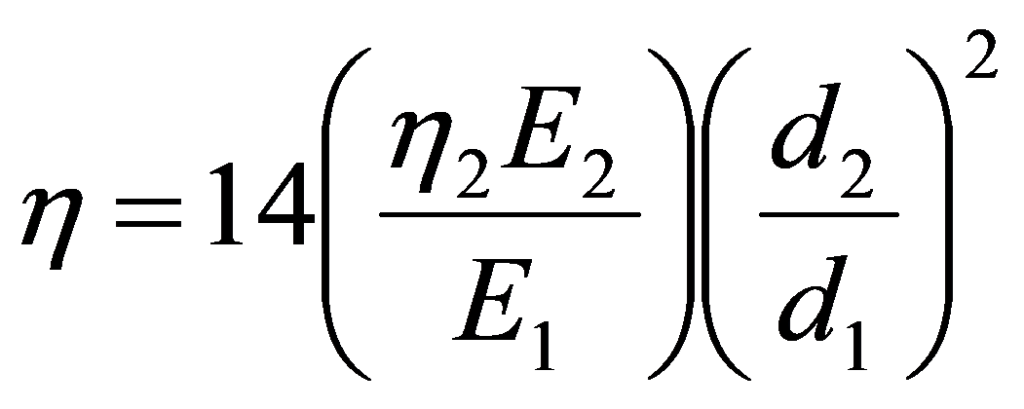
Onde se tem:

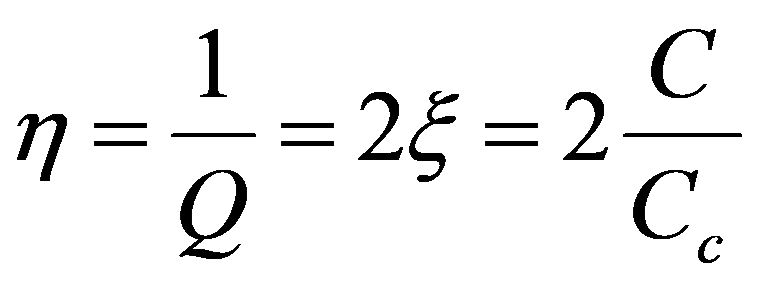
é o Fator de Perda da combinação do componente estrutural + material amortecedor

η₂         = Fator de perda do material amortecedor

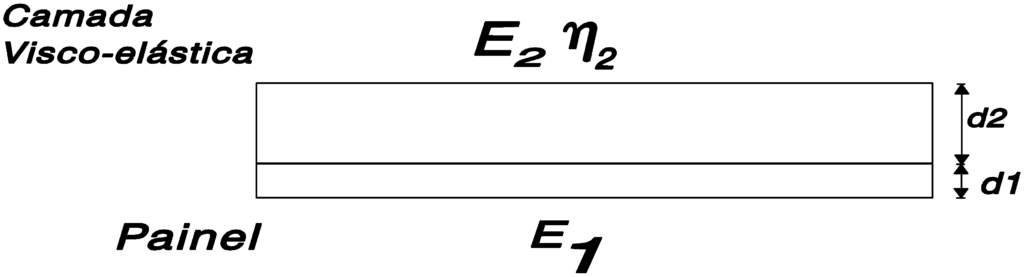
E₁ = Módulo de Elasticidade da componente estrutural

E₂ = Módulo de Elasticidade do material amortecedor

d₁ = Espessura da componente estrutural

d₂ = Espessura da camada de material amortecedor

Um facto que se torna evidente a partir desta fórmula, é que a espessura relativa da camada de material amortecedor (d₂/d₁), desempenha uma função muito importante no amortecimento resultante. Na prática, esta razão é escolhida de modo a ficar na proporção de três para um. Também se constata que é geralmente vantajoso aplicar uma camada (espessa) de material amortecedor em vez de se dividir o material por duas camadas, uma de cada lado.

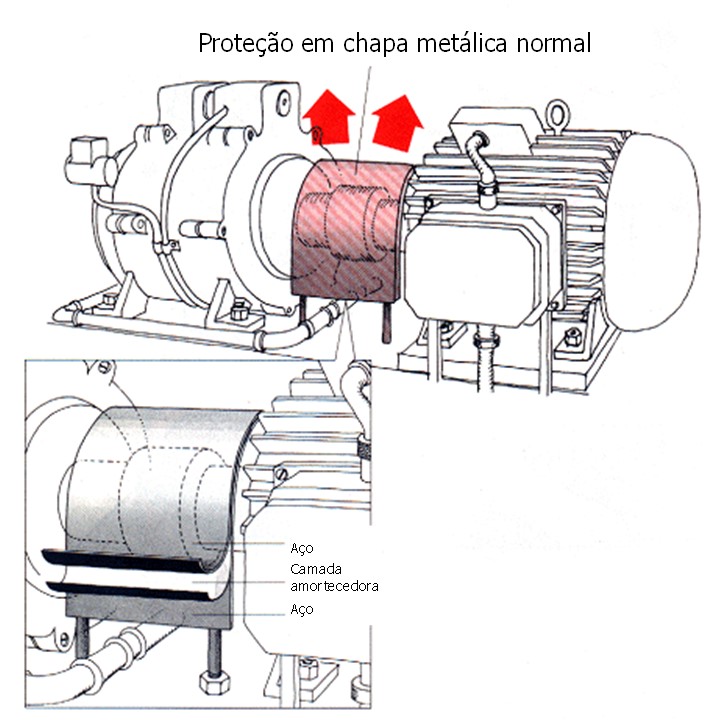
Um terceiro modo de se obter amortecimento em elementos estruturais é através da utilização de estruturas em sanduíche.

Existem diversos tipos de estruturas em sanduíche:

a) Estrutura com uma camada de material amortecedor coberta por uma folha de metal

b) Estrutura com uma camada fina de material viscoelástico entre duas chapas metálicas iguais

c) Estrutura com uma camada espessa de material viscoelástico entre duas chapas

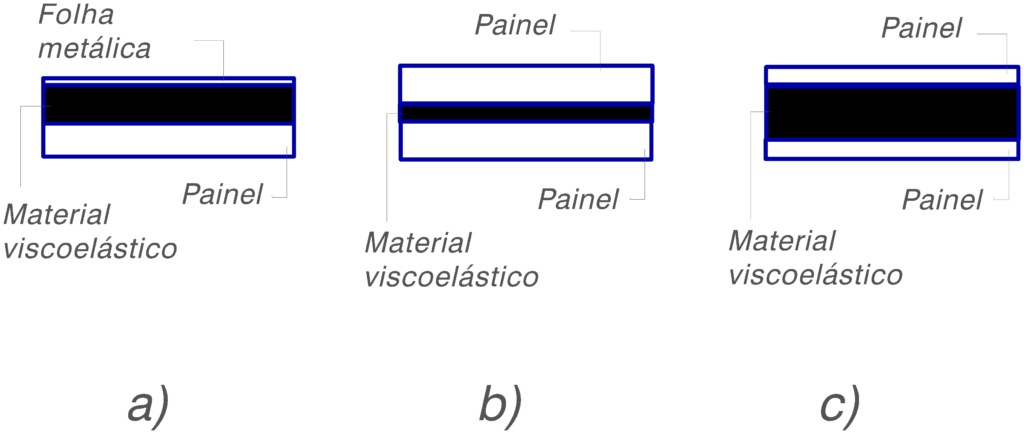
Nos materiais em sanduíche a espessura da camada do material viscoelástico não é muito importante. Parâmetro mais importante é a geometria global da estrutura (simétrica, assimétrica); as estruturas simétricas apresentam melhores características de amortecimento das vibrações. Por outro lado, quando a espessura da camada de material viscoelástico aumenta, também sobe a gama de temperatura e frequência em que se pode obter o amortecimento ótimo.

Na figura a seguir apresentada, vê-se um exemplo de aplicação de materiais amortecedores.