Analisador de vibrações 11 – Funções de 2 canais na frequência
O tema específico tratado em analisador de vibrações 11, consiste nas funções de 2 canais no domínio da frequência, num analisador de vibrações no âmbito de um programa de manutenção preditiva.
Quando se efetua análise de vibrações, para se tirar partido de todo o potencial de um analisador de vibrações, é necessário compreender o seu modo de funcionamento. Por isso, aqui são apresentados os conceitos de análise digital de sinal, implementados atualmente num analisador de vibrações FFT, do ponto de vista do utilizador quando efetua medição de vibrações.
Começa-se por apresentar as propriedades do Fast Fourier Transform (FFT) em que os Analisadores de Vibrações são baseados. Em seguida, mostra-se como essas propriedades FFT podem causar algumas características indesejáveis na análise do espectro, como aliasing e fugas (leakage). Tendo apresentado uma dificuldade potencial com o FFT, mostra-se quais soluções são usadas para tornar os analisadores de vibrações em ferramentas práticas. O desenvolvimento desse conhecimento básico das características do FFT torna simples obter bons resultados com um analisador de vibrações numa ampla gama de problemas de medição.
Aqui pode-se ver a gama de analisadores de vibrações disponibilizados pela D4VIB.
- Qual é a relação entre tempo e frequência
- Como funciona a amostragem e digitalização
- O que é o Aliasing e que efeitos tem
- Em se usa e em que consiste o zoom
- Como se usam as janelas na forma de onda
- Para que servem as médias
- O que é a largura de banda em tempo real
- Para que serve o processamento em sobreposição (“overlap”)
- Em que consiste o seguimento de ordens
- O que é a análise do envelope
- As funções de dois canais no domínio da frequência
- O que é para que serve a Órbita
- Quais são as funções de um canal no domínio do tempo
- Em que consiste o Cepstro
- Quais são as unidades e escalas do espetro
11 Funções de 2 canais na frequência
11.1 A função de resposta em frequência
A função de resposta em frequência H(ω) no domínio da frequência e a função de resposta ao impulso h(t) no domínio do tempo são usadas para descrever as relações entrada-saída (força-resposta) de qualquer sistema, em que o sinal a(t) e b(t ) representam entrada e saída do sistema físico. O sistema é considerado linear e invariante no tempo. A função de resposta em frequência e a função de resposta a impulso são os chamados descritores do sistema. Eles são independentes dos sinais envolvidos.
Na tabela a seguir, podem-se ver as formulações típicas das funções de resposta em frequência.
| Rigidez dinâmica | Força/deslocamento |
| Flexibilidade (receptância) | Deslocamento/Força |
| Impedância mecânica | Força/Velocidade |
| Mobilidade mecânica | Velocidade/Força |
| Inércia dinâmica | Força/Aceleração |
| Acelerância | Aceleração/Força |
Nota: definições constantes na NP ISO 2041.
A seguir pode-se ver um vídeo sobre as função de resposta em frequência.
As funções de transferência são amplamente utilizadas na análise de sistemas mecânicos. Para isto é normal excitar a estrutura com um martelo ou excitador de vibrações e medir a resposta com acelerómetros.
Por exemplo, em estruturas mecânicas, as características da função de transferência mostrarão ressonâncias perigosas. A banda de frequência, onde a tensão do material é muito alta, deve ser evitada, por exemplo especificando uma velocidade de rotação a evitar. O processo simplificado funciona assim: um sinal de entrada é aplicado ao sistema e o sinal de saída é medido.
A divisão entre a resposta e a excitação basicamente fornece a função de transferência.
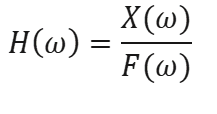Em que: ω = 2 π f
ou seja:
11.2 Como obter a função de transferência numa estrutura mecânica
- Excitar a estrutura com martelo ou excitador de vibrações medindo a força dinâmica;
- Medir a resposta com acelerómetros (aceleração)
- Calcular a função de transferência entre a entrada e a saída medidas do sistema
- Calcular a função de coerência. Se a coerência for 1, a resposta medida é causada totalmente pela entrada medida. Se a coerência for menor que uma em qualquer frequência, isso indica que a resposta medida é maior do que devido à entrada medida, ou seja que existe ruído na entrada ou na saída.
11.3 Funções de 2 canais no domínio da frequência – A função de coerência
A Coerência é função versus frequência, que indica quanto da saída é devido à entrada na FRF. Pode ser um indicador da qualidade da FRF. Avalia a consistência do FRF desde a medição até à repetição da mesma medição. O valor de uma função de coerência varia entre 0 e 1.
Assim a Coerência é um gráfico que representa a correlação entre dois sinais no domínio da frequência. Dois sinais são considerados coerentes se tiverem uma diferença de fase constante e a mesma frequência e forma de onda. O gráfico de coerência apresenta como o sinal de resposta está relacionado ao sinal de entrada. Os valores para coerência estarão entre 0 e 1, onde um valor 0 indica que não há relação entre os dois sinais e um valor 1 indica que há uma relação perfeita entre os dois sinais.
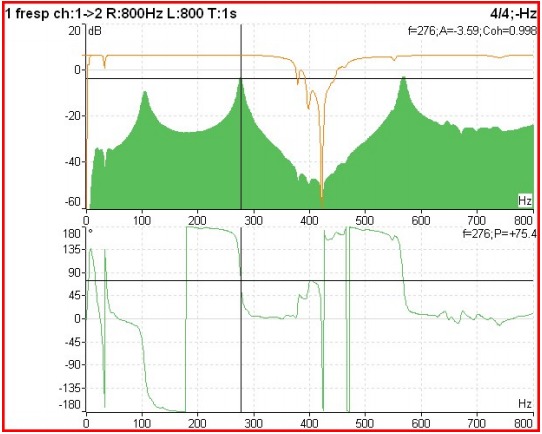
No gráfico a seguir apresentado a partir de um ensaio de impacto numa chumaceira de uma máquina em que se medio a resposta vibratória da estrutura a um choque gerado por um martelo instrumentado com um sensor de força pode-se a observar a:
- mobilidade mecânica (verde cheio, em cima)
- coerência (castanho, em cima),
- relação de fase (em baixo)
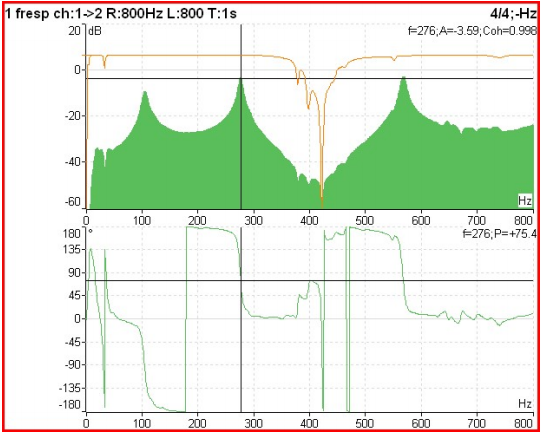
Funções de 2 canais no domínio da frequência – Figura 11.1 – A função de resposta em frequência, coerência e fase
Quando a amplitude de um FRF é muito elevada, por exemplo a uma frequência de ressonância, a coerência terá um valor próximo de 1. Quando a amplitude de um FRF é muito baixa, por exemplo a uma frequência de anti-ressonância, a coerência terá um valor próximo de 0. Isto porque como os sinais são muito pequenos, a sua repetibilidade é tornada inconsistente pelo nível de ruído da instrumentação. Isto é aceitável/normal. Quando a coerência está mais próxima de 0 do que 1 a uma frequência ressonante, ou em toda a gama de frequências, isto indica um problema com a medição. Os problemas podem incluir:
- Erro de instrumentação – Por exemplo, não está a ser fornecida energia ICP ao transdutor que requer energia ICP
- Excitação inconsistente – A estrutura não está a ser atingida por um martelo de impacto consistente (por exemplo, o operador está cansado e com uma estrutura impressionante em diferentes ângulos entre impactos)
- Força insuficiente – A estrutura não está a ser excitada. Por exemplo, um martelo muito pequeno (exemplo: tamanho de lápis) sobre um objecto grande (exemplo: tamanho de uma ponte) com uma grande distância entre a excitação e a medição da resposta
- Note que se for realizada apenas uma medição, a coerência será um valor de 1! O valor será um em toda a gama de frequências – dando a aparência de uma medição “perfeita”. Isto porque pelo menos duas medições FRF precisam de ser feitas e comparadas para começar a calcular uma função de coerência significativa.
11.4 A obtenção da função de transferência com um ensaio de impacto
Neste ensaio a estrutura em estudo é sujeita a um impacto, que irá excitar todas as suas frequências naturais, ficando depois a vibrar livremente. Para este fim é utilizado um martelo instrumentado que permite medir a força do impacto.
Este ensaio é efetuado com a seguinte instrumentação:
- Analisador de dois canais
- Acelerómetro
- Martelo instrumentado com sensor de força
Funções de 2 canais no domínio da frequência – Figura 11.2 – Medição da função de resposta em frequência com um ensaio de impacto
A partir do sinal de aceleração, que mede a resposta da estrutura e do sinal da força, introduzida na estrutura pelo martelo instrumentado, calculam-se três parâmetros:
- Função de resposta em frequência (FRF);
- Fase entre canais;
- Coerência entre canais.
Aqui pode ver um vídeo sobre o ensaio de impacto.
A função FRF é responsável pela determinação da resposta em frequência da estrutura. Para isso, a função FRF relaciona os dados de entrada com os dados de saída. Neste caso, a entrada consiste na força de excitação aplicada pelo martelo e a saída a vibração medida pelo acelerómetro, obtendo-se no final a relação entre os dois sinais, que dará a informação necessária para a identificação da frequência natural. A medição de fase, define inequivocamente que estamos na presença de uma frequência natural pois, na ressonância a fase varia 180º. Caso esta variação seja inferior a 180º quer dizer que, ou a estrutura está fortemente amortecida ou então, que o movimento da estrutura na ressonância não ocorre na direção do acelerómetro e/ou do martelo. A coerência entre os sinais é uma medição que tem como fim validar o ensaio de impacto, estabelecendo a relação entre quanto da vibração de saída (resposta) foi provocada pela excitação externa (força aplicada pelo martelo), ou seja, caso toda a vibração de saída seja provocada pelo impacto do martelo o valor da coerência seria 1. No caso do valor de coerência do teste ser superior a 0,75, a recolha pode ser considerada válida. Caso seja inferior a 0,75 quer dizer que a vibração não foi só provocada pelo impacto do martelo, mas também, por outras forças externas.
Conforme já foi referido no ponto 5, neste ensaio utiliza-se uma janela uniforme para o sinal do martelo (gráfico superior com o sinal medido e a janela) e uma janela exponencial para o sinal do acelerómetro (gráfico inferior) como se pode ver na figura a seguir apresentada.
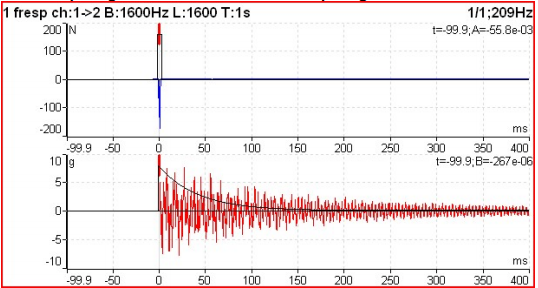
Funções de 2 canais no domínio da frequência – Figura 11.3 – Janelas para o ensaio de impacto
Aqui pode ver um vídeo com a prática deste ensaio.
11.5 A fase entre canais
A fase entre canais da função de transferência, pode ser utilizada para se conhecer o movimento relativo de duas chumaceiras ou partes de máquina, sem tacómetro.
A seguir pode-se ver um exemplo de utilização de medição de fase entre canais (a 1x RPM) para verificar onde existem desapertos. Em juntas bem apertadas a fase é aproximadamente igual. Se existir um desaperto isto não ocorre.
Funções de 2 canais no domínio da frequência – Figura 11.4 – A medição da fase para identificação de desapertos.
