aislamiento de vibraciones
aislamiento de vibraciones
En este artículo, el tema del aislamiento de vibraciones y reglas de montaje, revisar el tema de los sistemas con cierto grado de libertad.
1 – DESCRIPCIÓN DE UN SISTEMA DINÁMICO SIMPLE
1.1 – introducción
Los sistemas que se describirán a continuación son los siguientes:
– Movimiento libre con un grado de libertad, no amortiguado
– Movimiento libre con un grado de libertad, acolchado
– Movimiento forzado con cierto grado de libertad, no amortiguado
– Movimiento forzado con cierto grado de libertad, acolchado
En verdad, todos los sistemas físicos tienen un número infinito de grados de libertad.. Sin embargo, un análisis preliminar mostrará que algunos componentes del movimiento son, o insignificante o poco interesante y puede suprimirse inmediatamente con el fin de estudiar el fenómeno que se va a observar. Esto reduce el número de grados de libertad a estudiar..
1.2 – Conceptos básicos
Una máquina se puede representar como un sistema de masas metroyo, unidos por elementos de rigidez Ki, poseyendo una humectación Allí.
Recordemos estas nociones.
PULPA
Una masa es un cuerpo rígido cuya aceleración, según la ley de Newton, es proporcional a la resultante de las fuerzas que actúan sobre él.

La unidad de masa es Kg o Ns² / m.
RIGIDEZ
Consideremos un resorte lineal:

La variación en la longitud del resorte es proporcional a la fuerza que se le aplica..
F = K (x-u)
Se considera un resorte ideal sin masa.. La fuerza que actúa en un lado es igual y opuesta a la fuerza que actúa en el otro lado. La constante de proporcionalidad k se llama rigidez del resorte..
La unidad en la que se expresa k es N / m.
MOJADURA
Considere un sistema de amortiguación viscoso como el que se muestra a continuación.
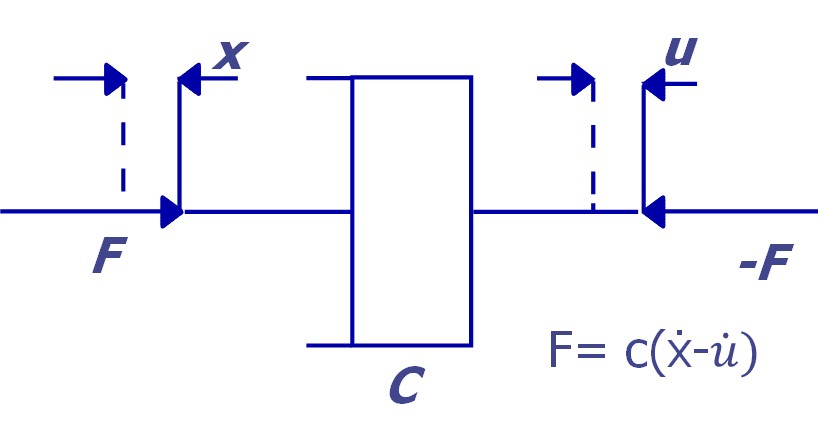
En amortiguamiento viscoso, la fuerza aplicada es proporcional a la velocidad relativa del punto de aplicación.
![]()
La unidad en la que se expresa C es Ns / m.
La constante C es el coeficiente de amortiguación, parámetro característico de un amortiguador. Se considera un amortiguador sin masa ideal. La fuerza que actúa sobre un lado es igual y opuesta a la que actúa sobre el centro..
Por lo tanto, las ecuaciones características se pueden escribir en general de la siguiente manera:

Otras definiciones que deben tenerse en cuenta son las siguientes:
| movimiento libre – | Movimiento sin fuerza externa |
| Movimiento no amortiguado – | Movimiento sin efecto amortiguador |
| Movimiento con un grado de libertad – | Movimiento solo en una dirección |
1.3 – Movimiento libre no amortiguado con cierto grado de libertad
Considere, por ejemplo, un sistema que consiste en una masa M conectada a un punto fijo por un resorte K. También considere que la masa solo puede moverse en una dirección..
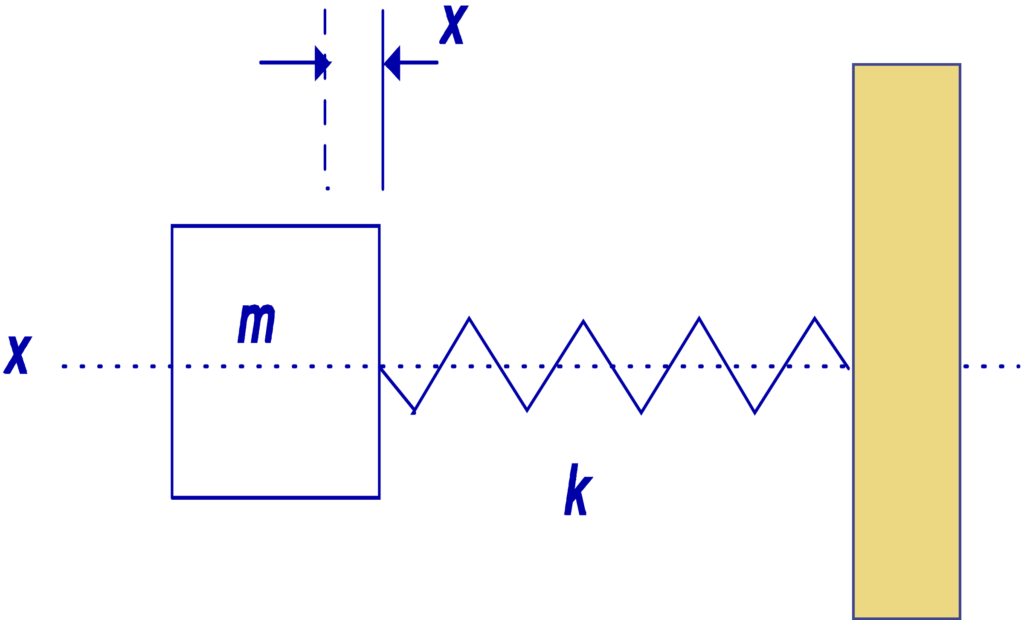
La ecuación que describe el movimiento de masa es:
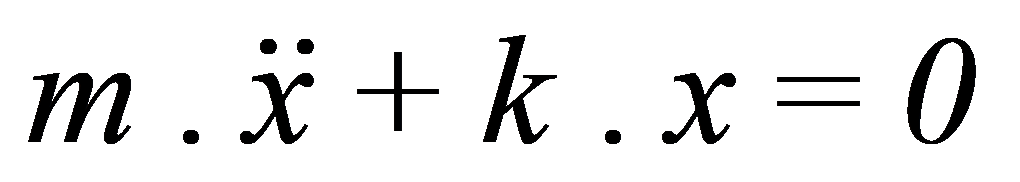
La solución a esta ecuación es:
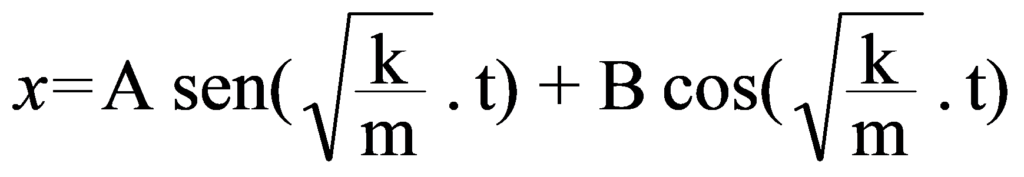
A y B son dos constantes que se pueden determinar a partir de las condiciones iniciales de velocidad y desplazamiento cuando t = 0.
Este movimiento es, por lo tanto, tipo sinusoidal cuya frecuencia es:
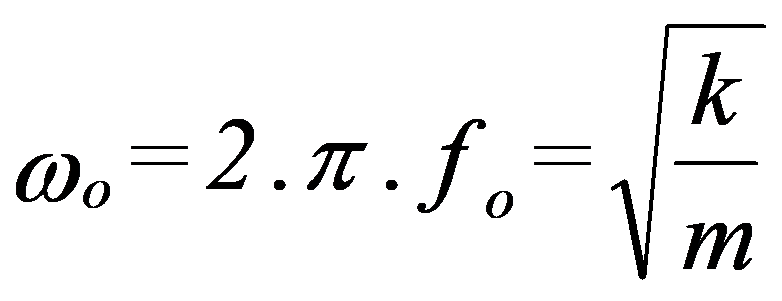
Esta frecuencia se llama frecuencia natural o frecuencia propia del sistema..
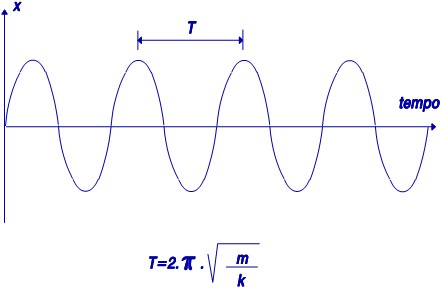
Si no hay amortiguación, este sistema permanecerá en movimiento indefinidamente como se puede ver en la figura..
El ejemplo de las fuerzas en una máquina rotatoria
La causa raíz de la vibración excesiva, más frecuente en las máquinas es la excentricidad de masa. La excentricidad de la masa debe verse desde el punto de vista de la simetría del rotor., con respecto al reconocimiento del comportamiento natural después de la conservación del momento angular. El punto clave a reconocer es que cada objeto tenderá natural y libremente a girar alrededor de su verdadero centro de masa. (o eje de inercia) después de aplicar cualquier binario. Esto es impulsado por la inercia de las partículas que componen el objeto al iniciar el movimiento circular de rotación.. La única forma de evitar esta rotación alrededor del centro de masa) es cuando se impone alguna forma de fuerza de restricción sobre el objeto giratorio para mantenerlo en una rotación forzada, descentrado, que obliga al verdadero centro de masa a trasladarse lateralmente o girar alrededor del eje de rotación forzada.
Como resultado de esta asimetría rotacional impuesta, una parte de la energía total suministrada por el par de entrada para acelerar la masa del rotor se convierte en lo que finalmente se observa como “vibración” (mas precisamente, la deflexión radial y la traslación lateral del eje del muñón del rotor). Esta energía se manifiesta en la fuerza centrífuga generada por la inercia de cualquier parte de la masa giratoria que sea asimétrica., relativo al eje de rotación forzado/rotación. Esta fortaleza es lo que típicamente se reconoce como “desequilibrio” durante la rotación. En combinación con toda la fuerza centrífuga es el(s) fortaleza(s) de reacción de la(s) punto(s) de restricción, manteniendo esta forma forzada de rotación.
1.4 – Movimiento libre amortiguado con cierto grado de libertad
El amortiguamiento se debe a la aparición de fuerzas pasivas que se oponen a las velocidades.. La amortiguación viscosa, que se encuentra a menudo, tiene la gran ventaja de preservar la linealidad de las ecuaciones; de hecho, las fuerzas pasivas son proporcionales a la velocidad.
En caso de que se agregue un amortiguador entre la masa y el punto fijo, la característica ecuación de movimiento, en ausencia de fuerzas externas, es el siguiente:
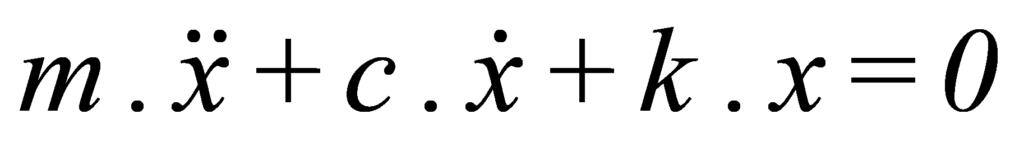
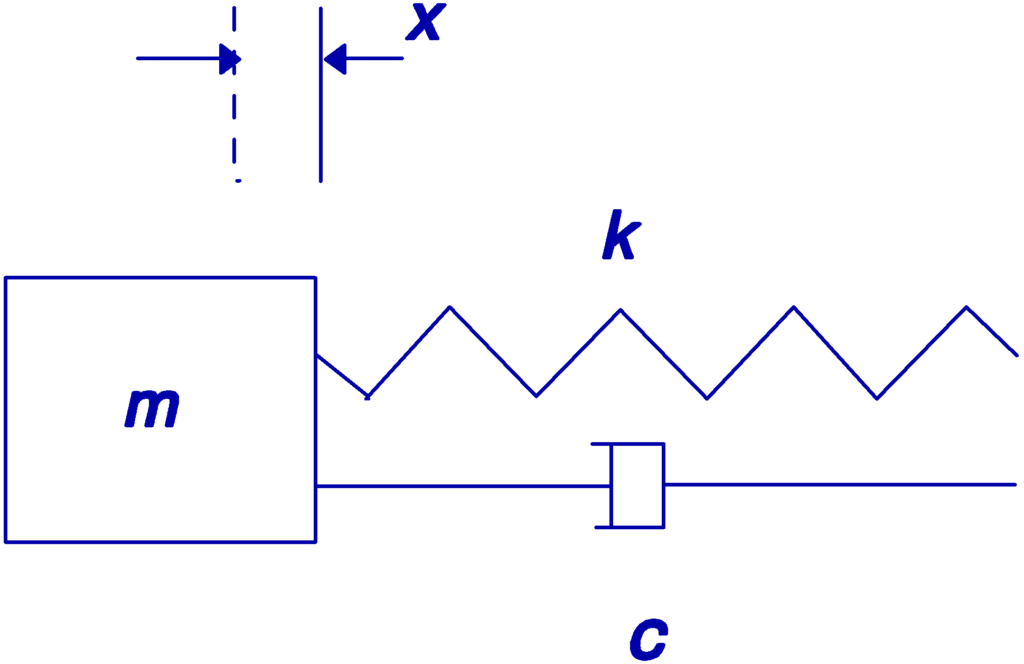
Normalmente se define un coeficiente llamado Coeficiente de amortiguamiento crítico y con el valor:
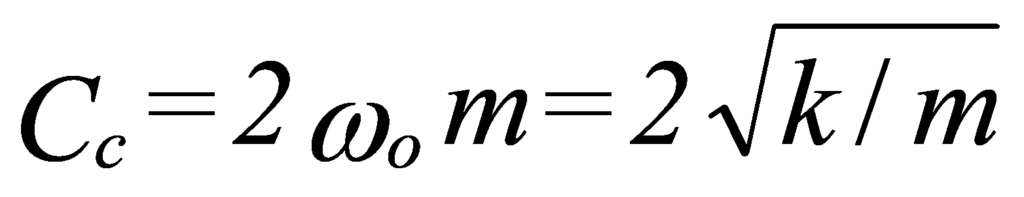
Según el valor de en relación con ξ, la ecuación presentará varias soluciones:
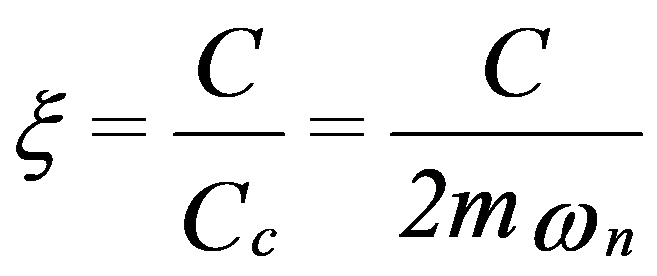
UNA) X<1 – movimiento subamortiguado
La solución de la ecuación viene dada por:
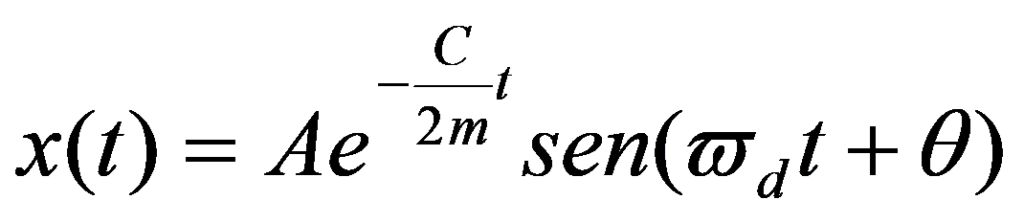
A = constante, función de las condiciones iniciales
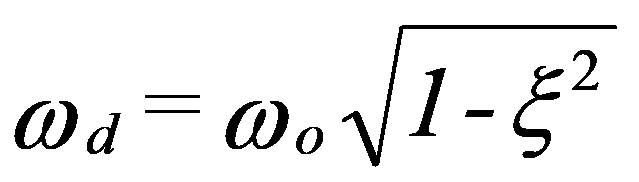
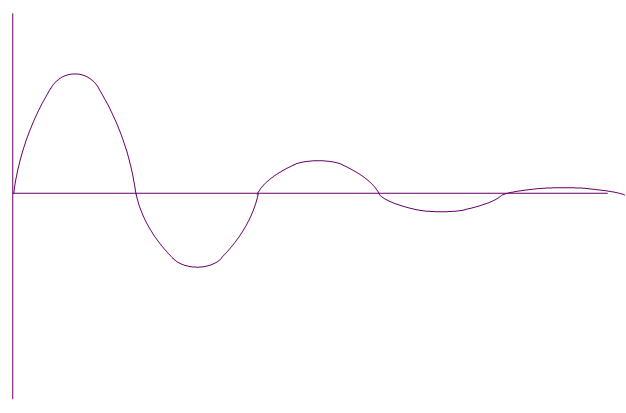
La evolución de este movimiento se puede ver en la siguiente figura.. Parece que el sistema tiende a volver a su posición de equilibrio tras sucesivas oscilaciones.. Las oscilaciones están moduladas por un exponencial decreciente.
B) ξ = 1 C = Cdo (amortiguación crítica)
No hay oscilaciones y el sistema tiende a su posición de equilibrio según la siguiente ecuación:
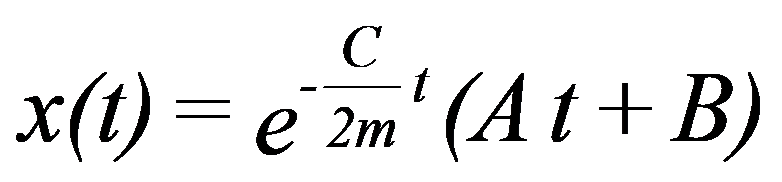
A y B son constantes que dependen de las condiciones iniciales.
do) X>1 do>dodo movimiento sobre-amortiguado
El movimiento tampoco es oscilatorio y se describe mediante la siguiente ecuación:
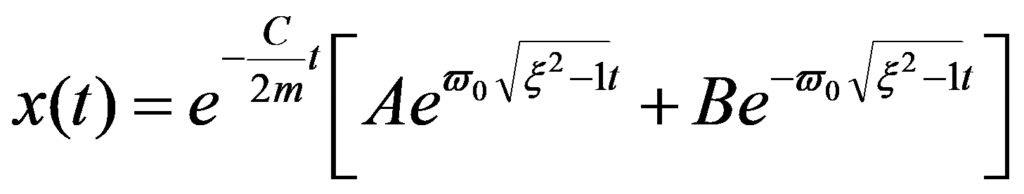
1.5 – Movimiento forzado con un grado de libertad no amortiguado y aislamiento de vibraciones
Un caso muy importante ocurre cuando se aplica una fuerza periódica a un sistema..
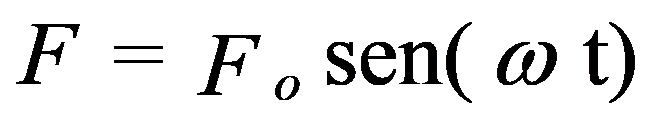
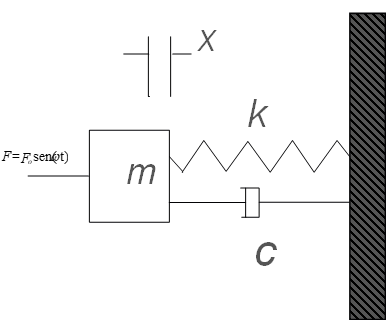
Este sistema puede, por ejemplo, representar una máquina con masa m conectada al suelo por una estructura con rigidez k.
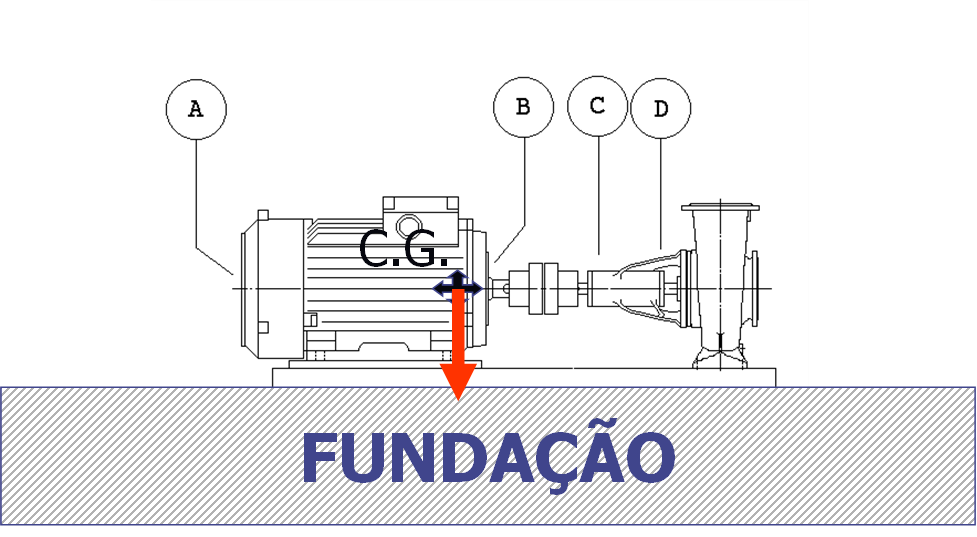
La fuerza F puede ser, por ejemplo, originado por un desequilibrio del rotor de la máquina que funciona a la velocidad de rotación.

La ecuación característica de este sistema se puede escribir de la siguiente manera:
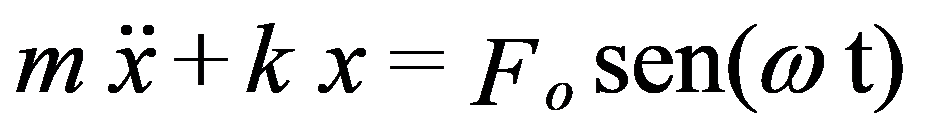
me que es la velocidad angular de la fuerza impulsora.
La solución a esta ecuación toma la siguiente forma:
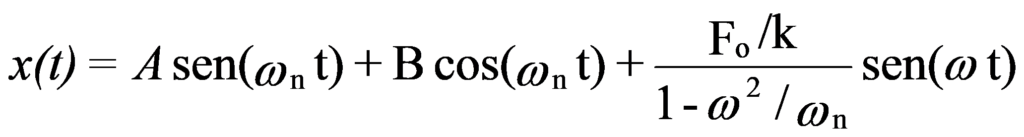
A y B son constantes en función de las condiciones iniciales.
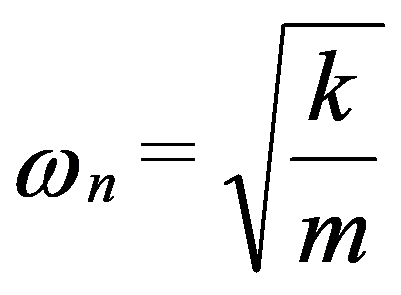
Los dos primeros términos representan una oscilación en la frecuencia propia ωnorte, exactamente de la misma manera que se determina para el movimiento libre no amortiguado. Ya se ha visto que debido al efecto amortiguador, esta oscilación desaparece al cabo de un tiempo.. permanecerá, por lo tanto, como la única solución estable una vibración forzada a frecuencia ω cuya amplitud será:
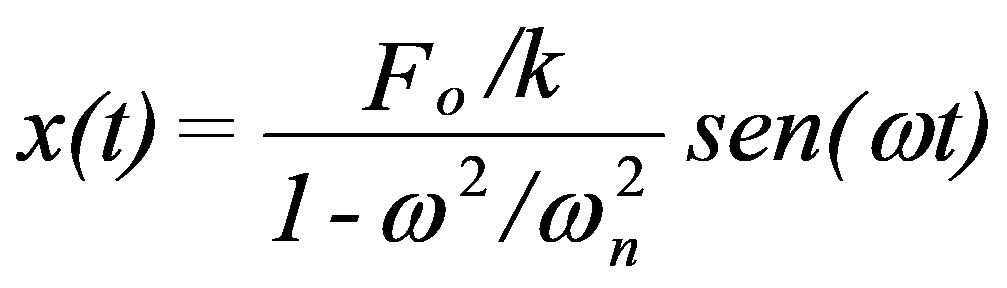
A continuación puede ver una demostración sobre la influencia de la masa., a frecuencia natural, un sistema con un grado de libertad.
1.6 – Movimiento forzado con cierto grado de libertad con amortiguación
Considere un sistema similar al anterior, pero ahora con un dispositivo de amortiguación.
Podemos volver a escribir la ecuación característica de este sistema:
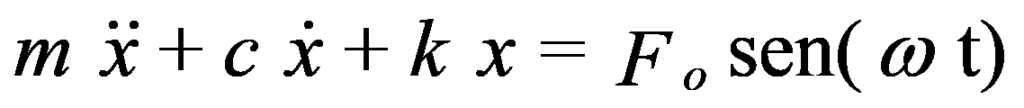
Cuando la amortiguación es distinta de cero (C ≠ 0), el desplazamiento x se puede describir de forma aproximada mediante las siguientes fórmulas.:
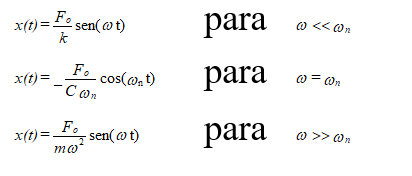
Estas son las soluciones estables, no entrar, por lo tanto, tener en cuenta las oscilaciones en la propia frecuencia del sistema que desaparecen después de algunas oscilaciones.
Parece que, cuando la frecuencia de la fuerza de excitación ω es igual a la frecuencia propia del sistema (segundo caso), la amplitud es inversamente proporcional a la amortiguación. En caso de amortiguación débil, Puede ser peligroso operar una máquina a una velocidad cercana a la propia frecuencia del sistema. (comúnmente conocida como velocidad crítica de la máquina) debido a que los niveles de vibración pueden alcanzar valores muy elevados.
La relación entre la respuesta resultante en amplitud x, y el desplazamiento que sufriría el sistema si la fuerza f se aplicara estáticamente XS t = f / k se llama factor de amplificación Q:
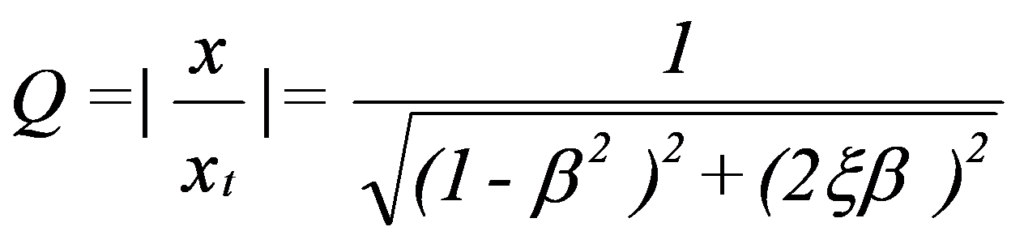
donde tiene usted:
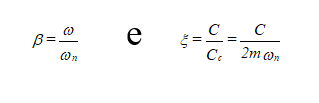
En la figura se puede ver la presentación gráfica de esta ecuación..
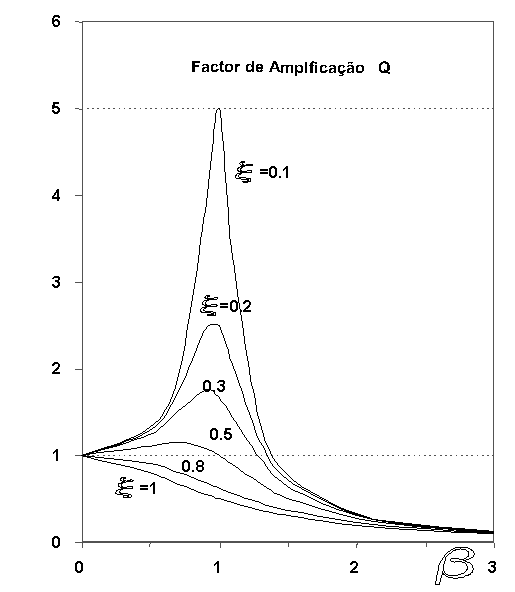
A continuación puede ver una demostración sobre la relación entre la fuerza de excitación y el rango de movimiento., en varias frecuencias, en un sistema con un grado de libertad.
2 – EL AISLAMIENTO DE VIBRACIONES
2.1 – Elección de soportes en aislamiento de vibraciones
En el caso del aislamiento de vibraciones, el parámetro que importa considerar es el relacionado con la fuerza transmitida a la cimentación o base de la máquina. Este parámetro es la transmisibilidad T.
Este parámetro expresa la relación entre la fuerza transmitida a la base Ft, y la fuerza de la emoción Fo.
La fuerza transmitida a la base por el resorte y el amortiguador es:
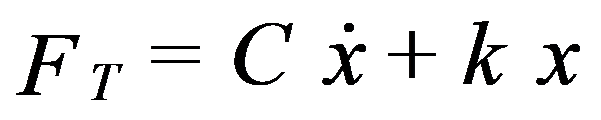
La transferibilidad viene dada por:
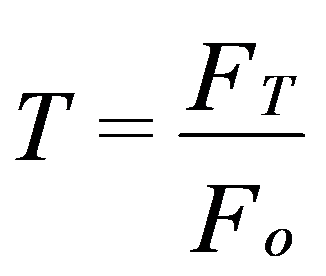
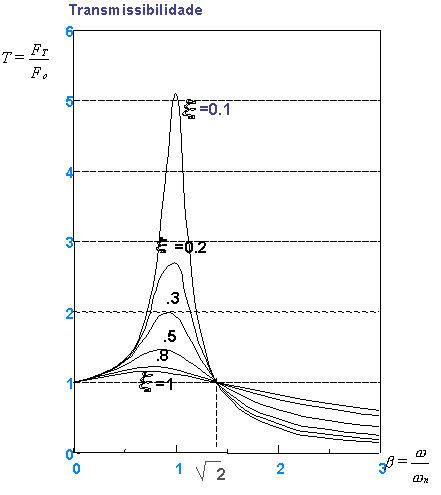
Cuando la relación ω / ωnorte = 1 (frecuencia del excitador = frecuencia propia del sistema), ocurre el fenómeno de resonancia y la transmisibilidad es muy superior a un. La amplitud de la respuesta del sistema. FT es por tanto superior a la excitación F0; hay una amplificación de las vibraciones.
Si la amortiguación del sistema es nula, la amplitud de la respuesta cuando ocurre la resonancia, se vuelve infinito.
En la práctica, la amortiguación C es generalmente más baja que la amortiguación crítica dodo..
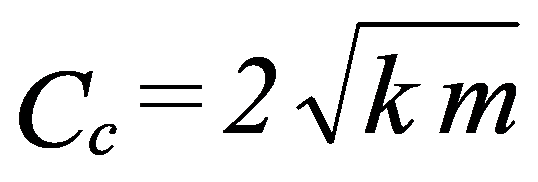
Tenga en cuenta que cuando se produce una resonancia, la amplitud disminuye cuando aumenta la amortiguación. para una relación Ohnorte < √2, T es mayor que uno y la amortiguación tiene una función de amortiguación.
Por lo contrario, Cuando Ohnorte > √2, hay una atenuación de la transmisión de potencia, o sea, cuando la frecuencia propia del sistema es menor que la frecuencia forzada. En este caso, sin embargo, la amortiguación tiende a aumentar la transmisibilidad. En este último caso, no se debe concluir que la amortiguación deja de ser interesante.; de hecho, su efecto no es demasiado grande para Ohnorte > √2 , y se puede compensar con resortes menos rígidos (o sea, reduciendo ωnorte). Además, incluso si no tiene la intención de operar la máquina en resonancia, puede haber situaciones excepcionales en las que esto ocurra y es fundamental tener amortiguación.
De esta forma, los cimientos se pueden aislar de una máquina insertando entre ellos un material elástico de tal manera que la frecuencia de la máquina sobre su soporte sea mucho menor. (al menos tres o cuatro veces) que la frecuencia fundamental de la fuerza periódica. Por supuesto, los armónicos serán más atenuados cuanto mayor sea su orden., especialmente si no hay gran amortiguación.
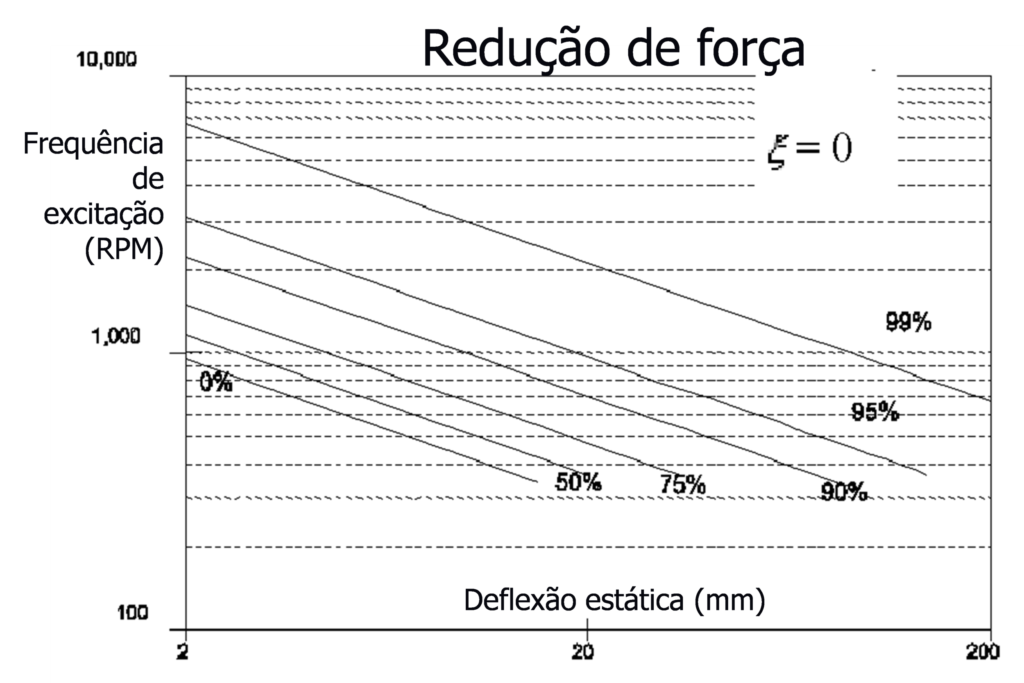
Un parámetro que se encuentra frecuentemente en los catálogos de proveedores de soportes antivibratorios es el Force Reduction.
reducción de fuerza (RF) = 1 – Transmissibilidade
Para obtener un aislamiento adecuado, la frecuencia natural ωnorte debe ser bajo (β = ω / ωnorte >1) y la amortiguación do debe ser reducido. Considerando así el caso de amortiguamiento nulo, la transmisibilidad es:

La Reducción de Fuerza vendrá entonces dada por:

cómo tienes:
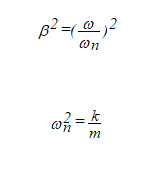
Siendo la deformación estática de un resorte:
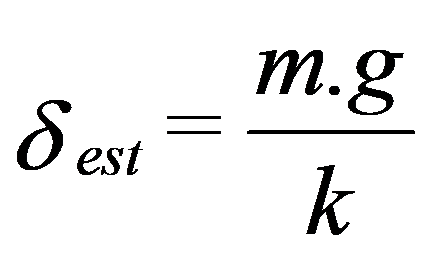
Se supone que la reducción de potencia será:
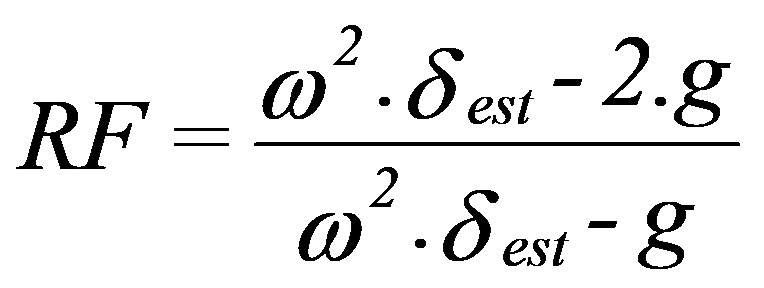
La siguiente figura muestra la representación de esta ecuación.
La eficiencia de un aislamiento se puede reducir significativamente si el sistema de aislamiento tiene conexiones rígidas a las estructuras vecinas., como pipas, perfiles, etc.. cualquier conexión, debe ser lo más flexible posible, tanto para aislar las vibraciones como para evitar que las conexiones se dañen.
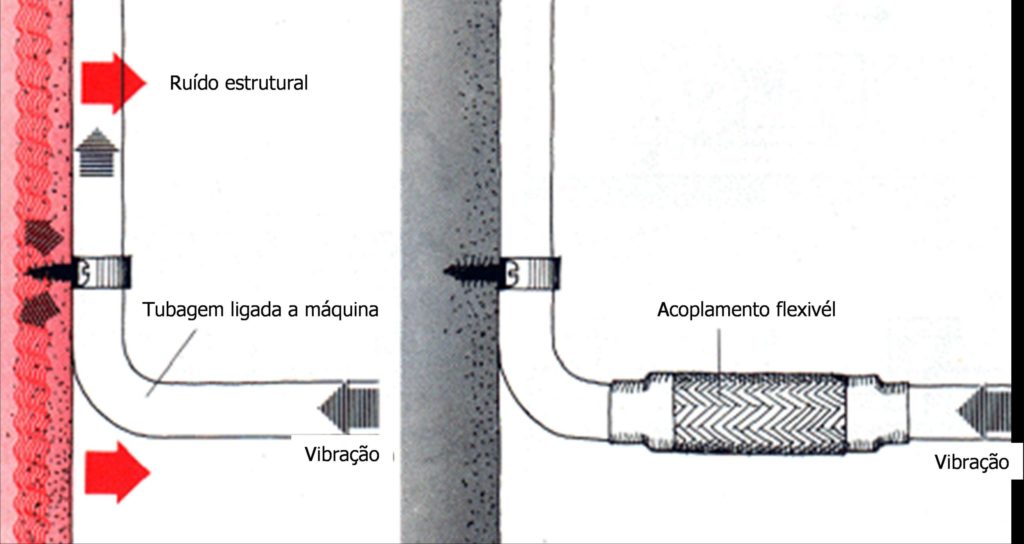
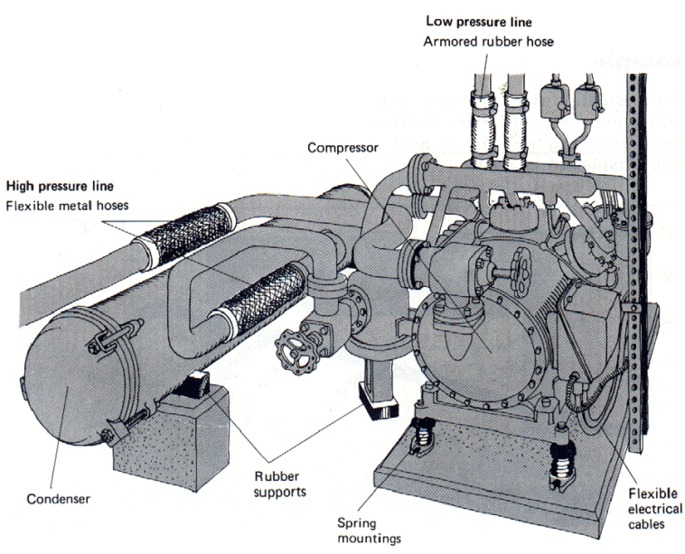
Este tipo de aislamiento antivibraciones, en el que se pretende que las vibraciones generadas en una máquina no se propaguen a la estructura sobre la que se apoya se denomina aislamiento activo.
Cuando el propósito del aislamiento es evitar que las vibraciones ambientales lleguen a una instalación en particular, se denomina aislamiento pasivo..
Algunas reglas practicas:
– Un aislamiento de 80 % de las vibraciones es suficiente
– Normalmente, la frecuencia natural del sistema compatible debe ser 1/3 o 1/4 de la frecuencia más baja para aislar que es normalmente la velocidad de rotación.
– Los soportes deben colocarse en los vértices de la base..
– Una vez instalados los soportes se debe verificar que la deflexión estática sea la misma para todos.
2.2 – El montaje – Posición de los soportes en relación con el centro de gravedad y aislamiento de vibraciones
Es sumamente importante que los soportes estén correctamente colocados en relación al centro de gravedad.. En la mayoría de los casos, todos los soportes son similares y se excitan por igual en amplitud y frecuencia.; para que estén correctamente instalados cuando tengan la misma deflexión en todos ellos. Por tanto, es muy importante que los apoyos estén distribuidos simétricamente en relación con el centro de gravedad y los principales ejes de inercia.. El incumplimiento de esta regla puede provocar excitación en dirección vertical., coincidir con movimientos en otras direcciones.
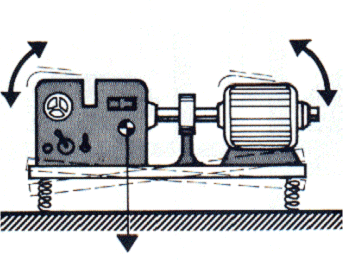
ocurrir, sin embargo, casos en los que este no es el caso y, por lo tanto, esto hay que tenerlo en cuenta.
1º Caso – Soportes conectados a puntos fijos en la máquina
Se debe ajustar la rigidez de los soportes..
PAG – Carga total
P1, P2 – Carga en soportes P1 y P2
K1, K2 – Rigidez de soporte 1 mi 2
delta – deflexión estática
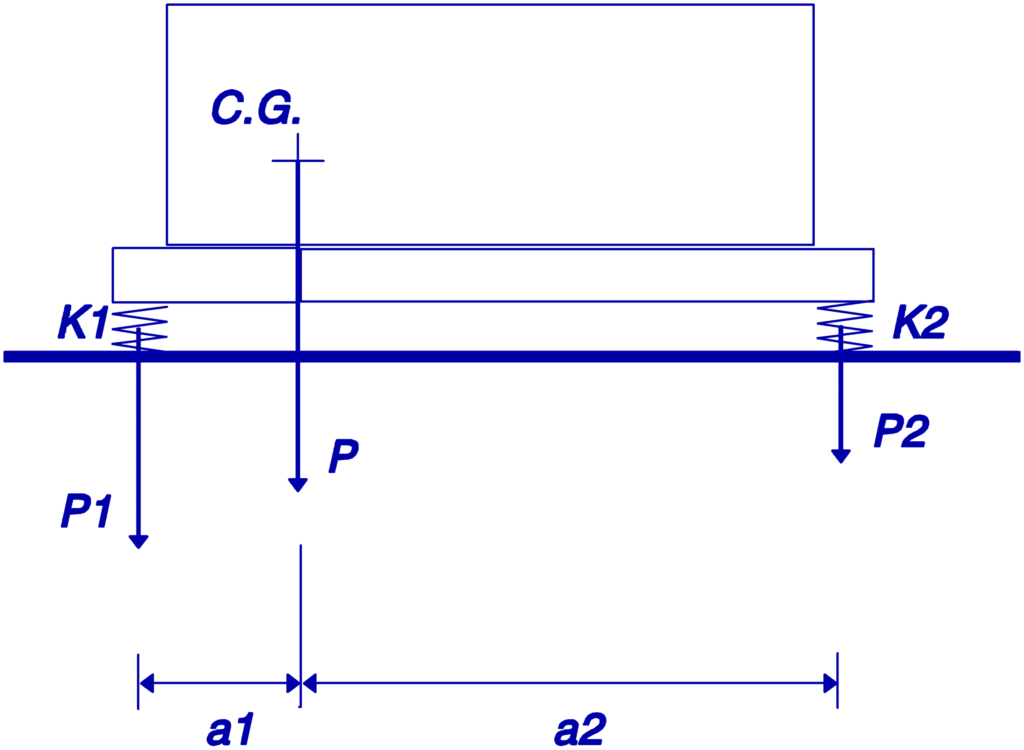
La condición de equilibrio es:
a1 × P1 = a2 × P2
entonces alli esta:
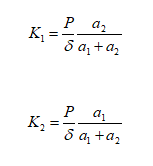
Luego deberá elegir soportes con una rigidez lo más cercana posible a K1 y K2..
2º Caso – Es posible elegir la posición de colocación de los soportes.
Se utilizan soportes idénticos y se colocan asimétricamente para recibir cargas iguales.
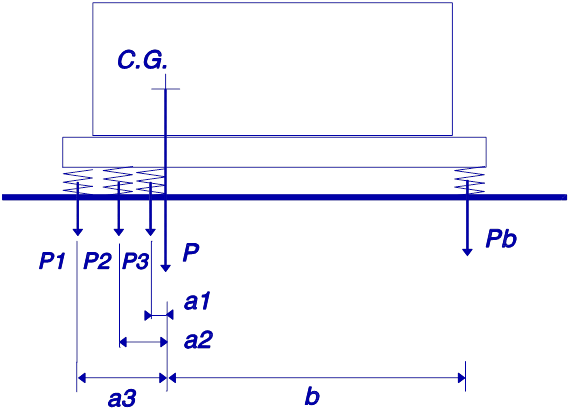
condición de equilibrio:
condición de equilibrio:
∑ (unayo. PAGyo) = ∑ (segundoj.PAGj)
Si todos los soportes son iguales, deben colocarse de manera que ∑unayo =∑bj.
Estas fórmulas asumen que la estructura basada en los soportes antivibratorios es rígida. Si la estructura no es rígida, la condición de equilibrio se puede encontrar experimentalmente.
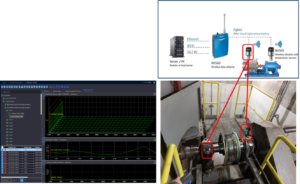
En este enlace puedes ver un ejemplo de los efectos de un fallo en el aislamiento de vibraciones.
2.3 – El bloque de inercia y aislamiento de vibraciones
El aislamiento de vibraciones se logra mediante la frecuencia natural y la amortiguación del sistema de soporte.. Entonces la función del bloque de inercia no es aislar vibraciones.
El bloque de inercia tiene varias funciones.:
– Reducir la amplitud del desplazamiento debido a las vibraciones aumentando la relación entre la masa estática y las fuerzas dinámicas.. lo, por lo tanto, se utiliza cuando las fuerzas dinámicas son grandes o desea reducir el desplazamiento.
– Bajar el centro de gravedad para obtener un mejor equilibrio del sistema en caso de distribución de masa asimétrica.
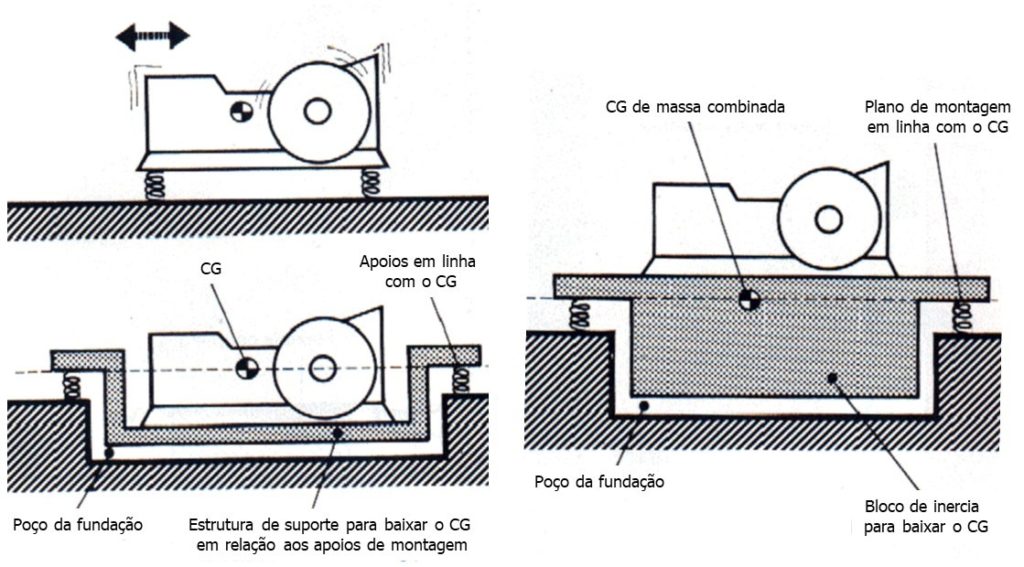
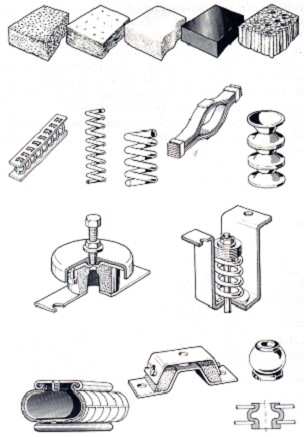
2.4 – Materiales utilizados en los soportes antivibratorios
Se utilizan muchos materiales en los soportes antivibratorios para el aislamiento de vibraciones.. Aquí solo vamos a hablar de algunos.
corcho
El corcho se utiliza tanto para compresión como para corte.. Sus propiedades dependen de la frecuencia y carga a la que está sometido.. Para cargas más grandes se vuelve más flexible.
muelles
Los resortes son los elementos elásticos que permiten mayores deflexiones estáticas, y en que, por lo tanto, si pueden alcanzar frecuencias más bajas. Posee, sin embargo, muy poca amortiguación también mostrando importantes desplazamientos. Soportar condiciones ambientales muy agresivas.
Goma
La mayoría de los soportes de goma funcionan al cortar para una mayor flexibilidad.. Sus propiedades varían mucho con la temperatura y la frecuencia.. Se degradan en presencia de aceite y gasolina..
Elastómetros Sintéticos
Los elastómetros tienen la ventaja de poder soportar fuerzas de tracción, a compresión y a cortar. Sin embargo, solo es difícil obtener ensamblajes con frecuencias inferiores a 5 hz.
3 – LA AMORTIGUACIÓN DE VIBRACIONES Y EL AISLAMIENTO DE VIBRACIONES
Las estructuras exhiben teóricamente un número infinito de resonancias. Si se somete a excitaciones de frecuencia variable o una banda de frecuencia amplia de vibraciones aleatorias, siempre se puede excitar un cierto número de resonancias.. Debido al hecho de que la mayoría de los materiales utilizados en ingeniería, como las cajas de aluminio y acero, tienen muy poca amortiguación interna, se hace necesario reducir los efectos de las resonancias con una acción externa. En el caso de las placas, a veces se utiliza la rigidización.. Sin embargo, este tipo de efecto no amortigua las resonancias.; sí transfiérelos a una frecuencia más alta. Si las frecuencias de resonancia se pueden transferir a un área donde no se excitan durante el uso normal del equipo, esta solución puede ser aceptable.
Por otro lado, en estructuras complejas, la transferencia de resonancias a otras frecuencias puede tener consecuencias nocivas en algunos componentes. Así, la solución más general para este tipo de problemas es aplicar algún tipo de amortiguación externa a los materiales..
La amortiguación externa se puede aplicar de varias formas:
una) A través de la amortiguación generada en la fricción superficial.
segundo) Mediante la aplicación superficial de un material de gran humectación
do) Uso de estructuras sándwich
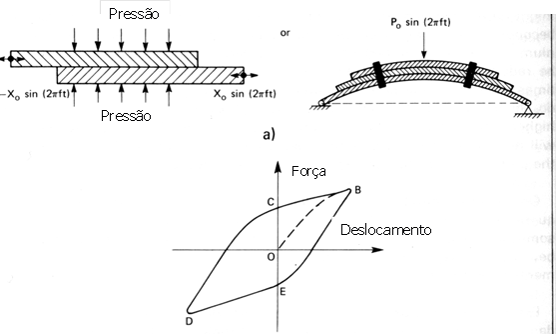
3.1 – Amortiguación de fricción
La amortiguación de la fricción se logra al permitir que dos superficies se deslicen una sobre la otra como se muestra en la Figura. Si no hay lubricante entre las dos superficies, el efecto de amortiguación es causado por la fricción seca.. La relación entre fuerza y desplazamiento., para este tipo de amortiguación, se muestra en la figura 22. La energía vibratoria así disipada viene dada por el área dentro de la curva B-C-D-E-B. Este tipo de amortiguación se utiliza en resortes de barra..
3.2 – Aplicación de materiales amortiguadores
Una de las formas más sencillas de introducir amortiguación en un componente de una estructura vibratoria es aplicar una capa de un material viscoelástico., con importantes pérdidas internas, en la superficie del componente. Este tipo de técnica de amortiguación se ha utilizado ampliamente en la industria del automóvil durante muchos años.. El material más conocido para este propósito se llama masilla., hecho de asfalto.
Este tipo de materiales, están hechos de polímeros, y tienen propiedades óptimas en una frecuencia y rango de temperatura dados..
Para obtener la mejor amortiguación del conjunto de componentes estructurales + material de acolchado, el factor de pérdida interna y el módulo de elasticidad del material amortiguador deben ser altos.
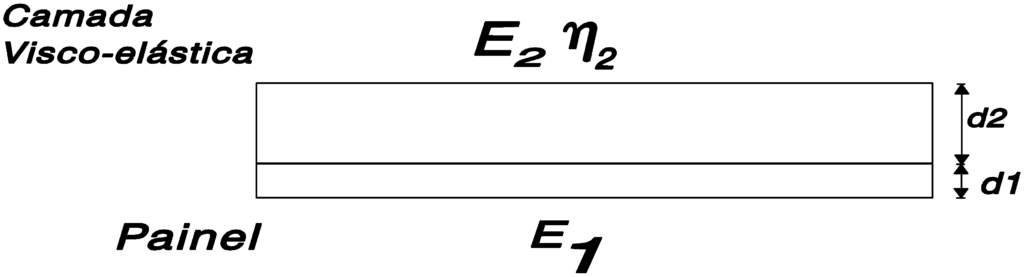
La siguiente fórmula aproximada describe las características de amortiguación de una superficie tratada.:
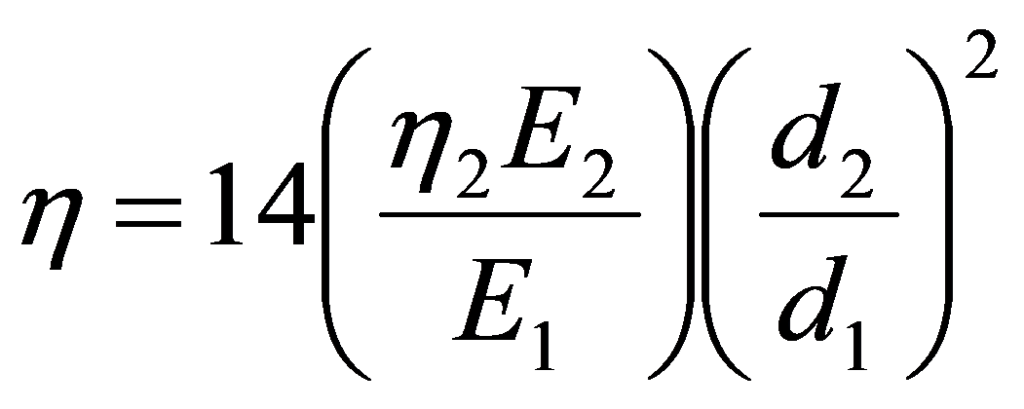
donde tiene usted:
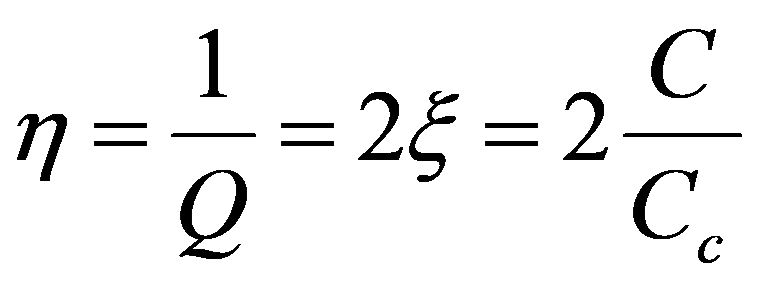
es el factor de pérdida de la combinación de componentes estructurales + material de acolchado
la2 = Factor de pérdida de material de amortiguación
mi1 = Módulo de elasticidad del componente estructural
mi2 = Módulo de elasticidad del material amortiguador
re1 = Espesor del componente estructural
re2 = Espesor de la capa de material amortiguador
Un hecho que se hace evidente a partir de esta fórmula., es que el espesor relativo de la capa de material amortiguador (re2/re1), juega un papel muy importante en la amortiguación resultante. En la práctica, esta relación se elige de modo que sea de tres a uno.. También se encuentra que, en general, es ventajoso aplicar una capa. (grueso) de material de amortiguación en lugar de dividir el material en dos capas, uno a cada lado.
Una tercera forma de obtener amortiguación en elementos estructurales es mediante el uso de estructuras sándwich.
Hay varios tipos de estructuras tipo sándwich.:
una) Estructura con una capa de material amortiguador cubierto por una lámina de metal
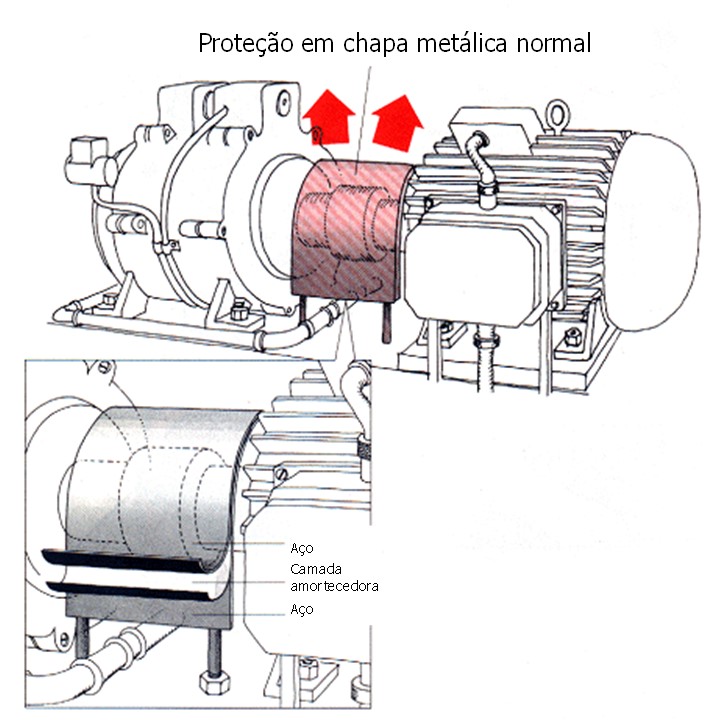
segundo) Estructura con una fina capa de material viscoelástico entre dos chapas idénticas
do) Estructura con una capa gruesa de material viscoelástico entre dos láminas
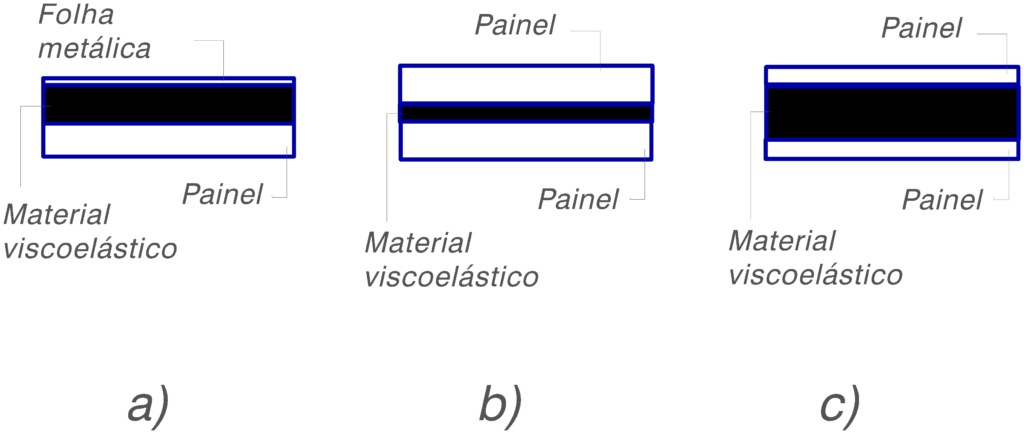
En los materiales tipo sándwich, el grosor de la capa del material viscoelástico no es muy importante.. El parámetro más importante es la geometría general de la estructura. (simétrica, asimétrico); Las estructuras simétricas tienen mejores características de amortiguación de vibraciones.. Por otro lado, cuando aumenta el espesor de la capa de material viscoelástico, también aumenta el rango de temperatura y frecuencia en el que se puede obtener una amortiguación óptima.
En la siguiente figura, ver un ejemplo de la aplicación de materiales amortiguadores.