Analizador de vibraciones 13 – Funciones de un canal en el tiempo
Analizador de vibraciones 13
El tema específico tratado en un analizador de vibraciones 13, consta de las funciones de un canal en el dominio del tiempo en un analizador de vibraciones.
Cuando se produceAnálisis de vibraciones, a través de la observación de los resultados de mantenimiento predictivo, para aprovechar todo el potencial de un analizador de vibraciones, necesitas entender cómo funciona. Por eso, aquí se presentan los conceptos de análisis de señales digitales, actualmente implementado en un analizador de vibraciones FFT, desde el punto de vista del usuario.
Comenzamos presentando las propiedades de la Transformada Rápida de Fourier. (FFT) en el que se basan los analizadores de vibraciones. En seguida, muestra cómo estas propiedades de FFT pueden causar algunas características indeseables en el análisis del espectro, como aliasing y breakouts (fuga). Haber presentado una dificultad potencial con la FFT, muestra qué soluciones se utilizan para hacer que los analizadores de vibraciones sean herramientas prácticas. El desarrollo de este conocimiento básico de las características de la FFT simplifica la obtención de buenos resultados con un analizador de vibraciones en una amplia gama de problemas de medición..
Aquí puede ver la gama deanalizadores de vibración puesto a disposición por D4VIB.
- ¿Cuál es la relación entre tiempo y frecuencia?
- Cómo funciona el muestreo y el escaneo
- Qué es el aliasing y qué efectos tiene
- Cómo se usa y en qué consiste el zoom
- Cómo se utilizan las ventanas de forma de onda
- ¿Cuáles son los promedios para
- ¿Qué es el ancho de banda en tiempo real?
- Para que sirve el procesamiento de superposición ("superposición")
- Que es el seguimiento de pedidos
- Que es el análisis de envolvente
- Las funciones de dos canales en el dominio de la frecuencia
- Para que sirve Orbit
- ¿Cuáles son las funciones de un canal en el dominio del tiempo?
- En qué consiste el Cepstro
- ¿Cuáles son las unidades y escalas del espectro?
13 - Analizador de vibraciones 13 - Funciones de un canal en el dominio en el tiempo
13.1 Analizador de vibraciones: medición básica de la amplitud de la forma de onda
La amplitud de la vibración, que es la característica que describe su severidad, Se puede medir de varias maneras. En la siguiente figura, uno puede ver la relación entre la amplitud pico a pico, o Pico, Medios de comunicación y el nivel efectivo (RMS).
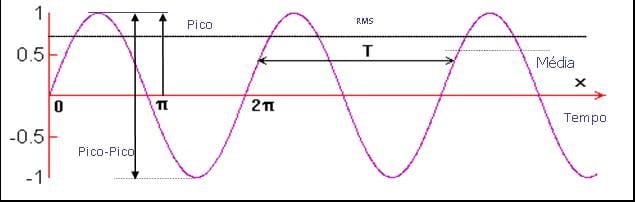Analizador de vibraciones 13 – Figura 13.1 Analizador de vibraciones: el nivel RMS, el pico y el pico-pico
El valor de pico a pico es importante en lo que indica la amplitud máxima de la vibración, que es un parámetro importante cuando se trata de saber, por ejemplo,, Desplazamientos máximos en máquinas herramienta o en medidas realizadas con transductores de desplazamiento..
El valor efectivo (RMS) Es el más utilizado porque tiene en cuenta un determinado intervalo de tiempo de medición y da un valor que está directamente relacionado con la energía de la vibración., o sea, su capacidad destructiva; es, por lo tanto, un valor promedio.
En la siguiente figura se puede ver que aparece tres formas de onda con la misma amplitud de pico y con diferentes valores efectivos. En un pulso de lengüeta llega a una condición sine, otra es una condición sine, otro es un sine truncada.
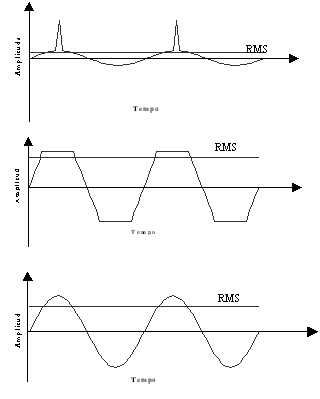Analizador de vibraciones 13 – Figura 13.2 - Analizador de vibraciones - Tres formas de onda con la misma amplitud máxima y con diferentes valores efectivos
Los impulsos que se pueden observar en la primera forma de onda, de la figura anterior, si se produjeron en una máquina rotativa corresponden a los choques. La medición de la amplitud máxima detecta mejor los choques o cualquier otro tipo de fenómeno impulsivo, la medición de la amplitud RMS, debido a este último ser un valor medio en un intervalo dado, mientras que el valor de pico es, por definición, la señal máxima en el tiempo. Para medir vibraciones sin amplitud de pulso efectiva (RMS) Es debido más adecuado para proporcionar un valor promedio. Para medir las vibraciones sinusoidales, cualquier, porque hay una relación fija entre la amplitud de pico y la RMS.
13.2 El factor de la cresta
El factor de cresta es el resultado de la división entre el valor pico y el valor RMS de la vibración y es una técnica para caracterizar la "impulsividad" existente en una forma de onda..
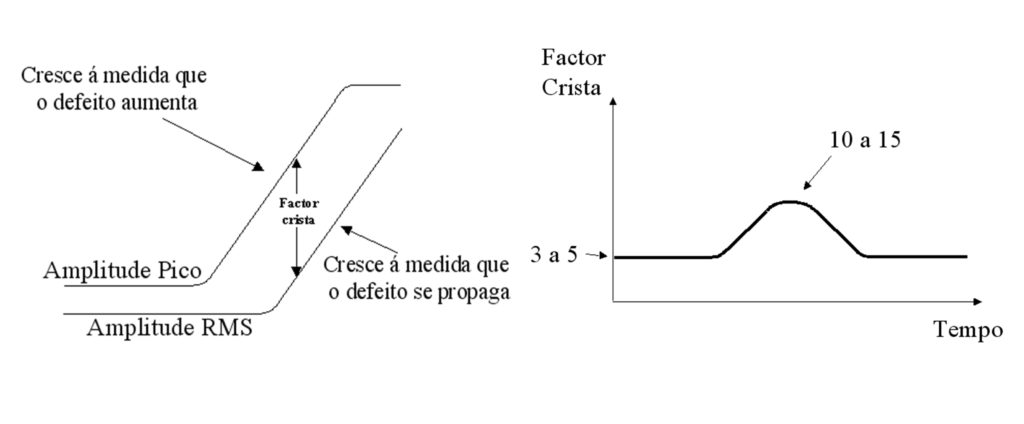Analizador de vibraciones 13 – Figura 13.3 - Analizador de vibraciones - El factor de cresta
Las curvas en la figura de arriba muestra una evolución típica de factor de cresta como la condición de funcionamiento de los cojinetes deteriora. Inicialmente, hay una relación relativamente constante entre el valor de pico y el valor RMS. El valor de pico crecerá normalmente hasta un cierto límite. Como los deteriora cojinete, más pulsos se generarán para cada paso de las bolas, en última instancia, influir en los valores RMS, a pesar de que la amplitud individual de cada pico no es mayor. Hacia el final de la vida del rodamiento, Factor de cresta puede haber bajado a su valor original, aunqué, sin embargo, pico y RMS valores han crecido considerablemente. Se presenta la mejor manera de presentar los resultados de las medidas; los valores de pico y RMS en el mismo gráfico, factor de cresta con la deducida a partir de la diferencia entre las dos curvas.
13.3 O curtosis
La curtosis es un indicador estadístico de la aparición de grandes picos en una forma de onda. (impulsividad). No mundo real, muchos tipos de vibración se caracterizan por señales con un alto valor de curtosis (en relación con la señal aleatoria gaussiana). El potencial de fatiga y daño de estas vibraciones es mayor que una réplica gaussiana pura.. La curtosis se puede expresar como un valor "K" normalizado dividiendo el cuarto momento estadístico dividido por el cuadrado del segundo momento estadístico. La siguiente ecuación muestra el cálculo de curtosis para N muestras.
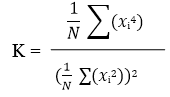
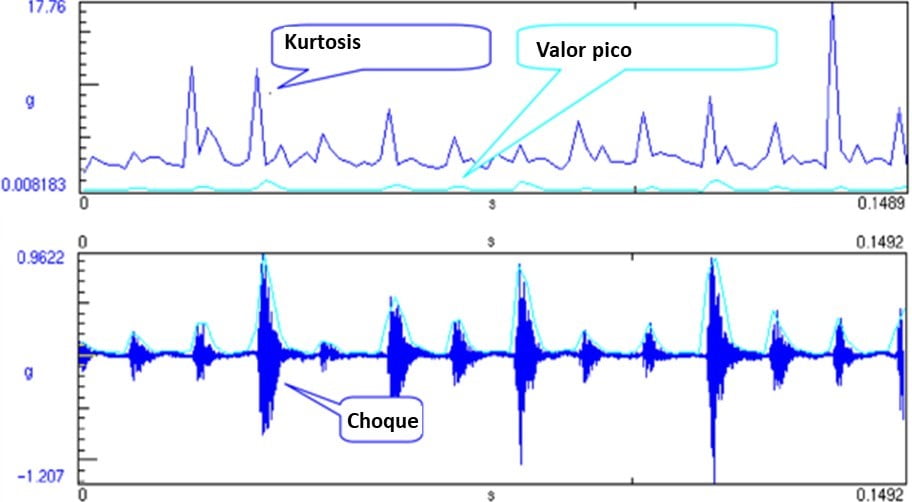
Analizador de vibraciones 13 – Figura 13.4 - Analizador de vibraciones - Forma de onda, valor pico y curtosis
13.4 Asimetrías en la amplitud de la forma de onda.
Observe la simetría de los datos de la forma de onda., por encima y por debajo del eje de la línea central, es importante. Los datos simétricos indican que el movimiento de la máquina es uniforme en cada lado de la posición central. Los datos no simétricos de la forma de onda del tiempo indican que el movimiento posiblemente esté restringido por la desalineación, fricción u otra fuerza externa.
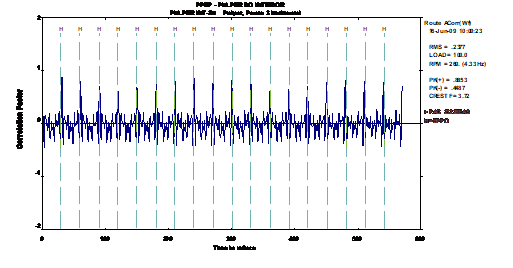Analizador de vibraciones 13 – Figura 13.5 - Analizador de vibraciones - Forma de onda asimétrica generada por impactos en un rodamiento
13.5 La media sincrónica de la forma de onda
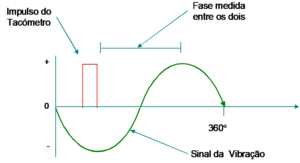
Como se mencionó en detalle en 6.3, esta técnica consiste en realizar medidas de la forma de onda, sincronizado con la rotación de uno de los ejes y la ejecución de una media de estas medidas. Como resultado de esta sincronización, eventos asincrónicos con la realización de la media, tienden a cero, mientras que el sincronismo se vuelve más visible. por lo tanto, la parte periódica de la entrada siempre será exactamente la misma en cada bloque de tiempo que tomemos, mientras el ruido, claro que sí, variará. Si sumamos una serie de estos bloques de tiempo activados por el tacómetro y dividimos por el número de bloques que tomamos, calculemos lo que llamamos una media lineal en el dominio del tiempo. Con esta técnica podemos eliminar las vibraciones que no están relacionadas con el eje de la forma de onda en la que se encuentra el tacómetro., como por ejemplo puedes ver a continuación , en la figura 13.6 para identificar un hueco en un engranaje.
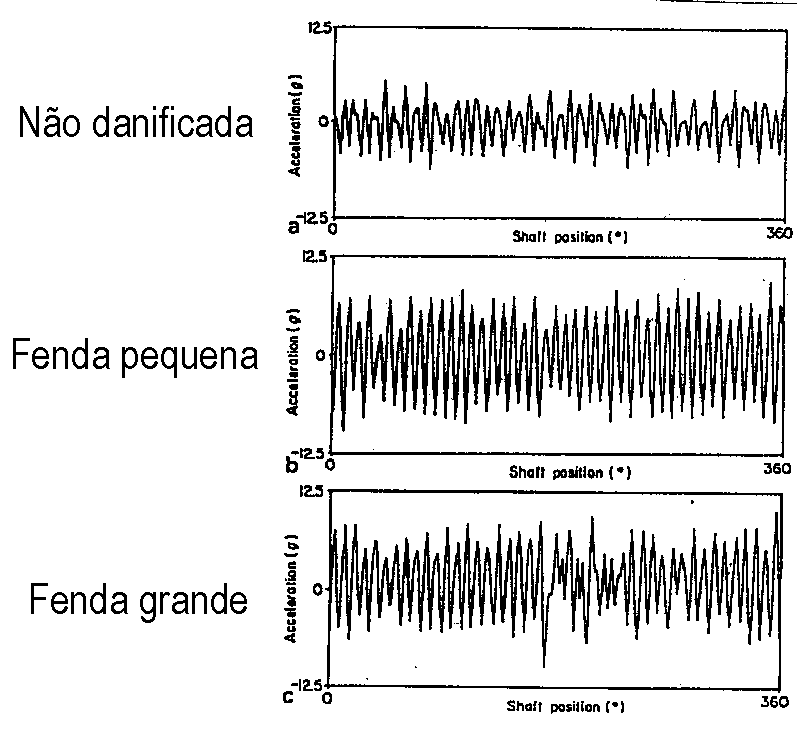
Analizador de vibraciones 13 – Figura 13.6 - Analizador de vibraciones - Detección de grietas en engranajes a través del Promedio Sincrónico de la Forma de Onda
Para la implementación de esta técnica se requiere la existencia de un sensor taquimétrico que informe permanentemente al equipo de medición sobre la velocidad de rotación del eje donde se están realizando las mediciones. Para la implementación de esta técnica se requiere la existencia de un sensor taquimétrico que informe permanentemente al equipo de medición sobre la velocidad de rotación del eje donde se están realizando las mediciones.. Esta técnica se ha aplicado tradicionalmente a engranajes complejos y altamente responsables como los helicópteros para determinar los defectos de los dientes., y en prensas de máquinas papeleras o laminadores para determinar la fuente de vibraciones con el fin de evitar problemas de calidad. Permite, por ejemplo, en dos rodillos de una prensa girando a la misma velocidad, distinguir las vibraciones generadas por un, de las vibraciones generadas por el otro, como se ilustra en la Figura 13.7
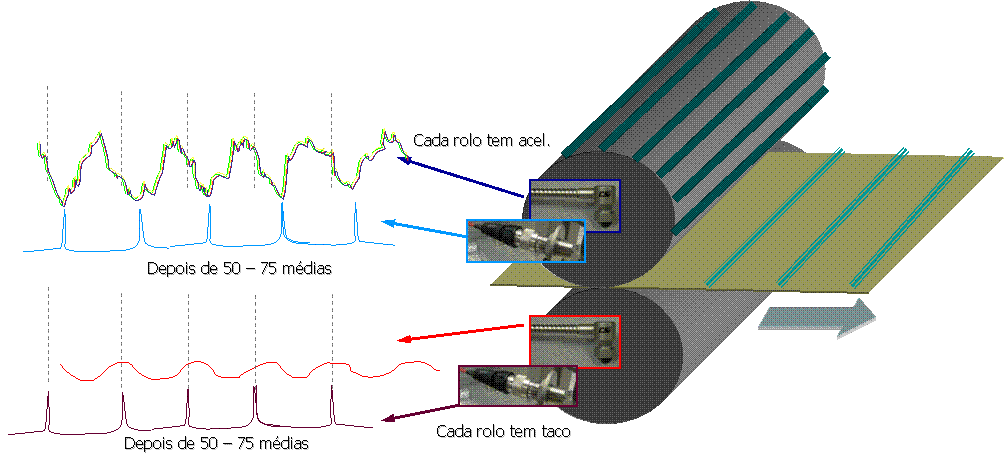Analizador de vibraciones 13 – Figura 13.7 - Implementación de promedio síncrono en rollos de prensa de máquinas de papel
La sincronización de medidas actúa como un filtro que nos permite observar / separar exclusivamente las vibraciones de una fuente de las otras..
13.6 Analizador de vibraciones 13 - Autocorrelación
La autocorrelación es una técnica de correlación que involucra solo una señal, y proporciona información sobre la periodicidad de la señal en el dominio en el tiempo. Autocorrelación, aparece así, como alternativa al análisis espectral. Las principales características de esta función son:
• la capacidad de identificar eventos de baja repetición,
• la capacidad de identificar y separar eventos periódicos de eventos aleatorios.
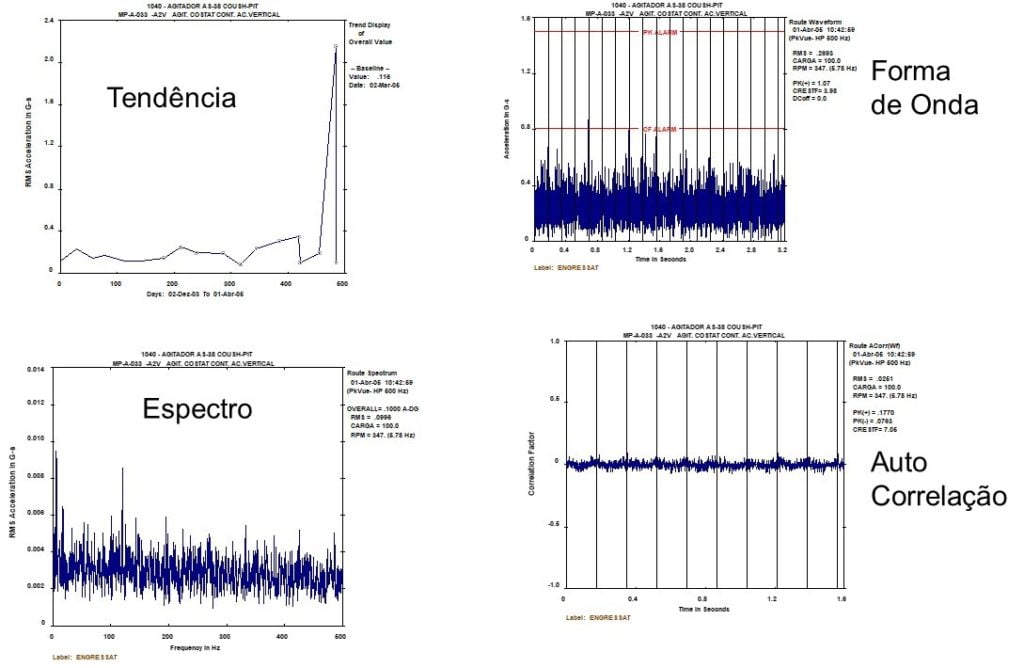
Analizador de vibraciones 13 – Figura 13.8 - Analizador de vibraciones - Aplicación de la función de autocorrelación para identificar la ausencia de periodicidad, o sea, el carácter aleatorio de una señal de vibración cuando ocurre un problema de lubricación en un rodamiento
Un analizador de vibraciones generalmente tiene la capacidad de mostrar la marca de tiempo en su pantalla.. Esta es la misma forma de onda que veríamos con un osciloscopio., una vista de dominio de tiempo de la entrada. Pero hay otras medidas en el dominio del tiempo que un analizador de vibraciones también puede tomar. Estas se denominan medidas de correlación.. Comencemos esta sección definiendo la correlación y, en seguida, le mostraremos cómo realizar estas medidas con un analizador de vibraciones.
La correlación es una medida de la similitud entre dos cantidades. Para comprender la correlación entre dos formas de onda, Comience multiplicando estas formas de onda en cada instante y sumando todos los productos.. Se, como en la figura 13.9, las formas de onda son idénticas, cada producto es positivo y la suma resultante es grande.
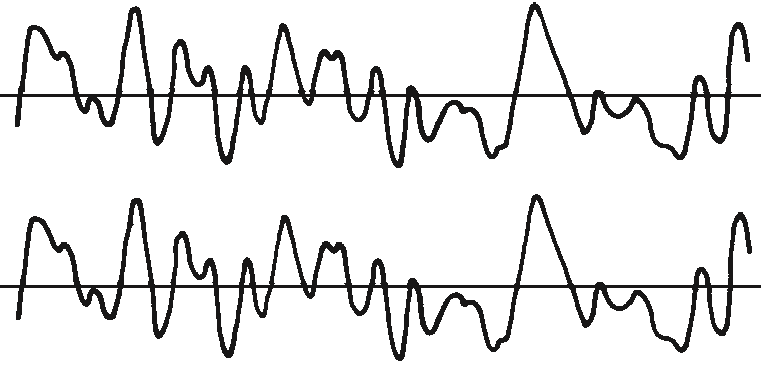Analizador de vibraciones 13 – Figura 13.9 - Analizador de vibraciones - Correlación de dos vibraciones idénticas
Se, sin embargo, como en la figura 13.10, los dos registros son diferentes, por lo que algunos de los productos serían positivos y otros negativos. Habría una tendencia a que los productos se cancelen, por lo que la suma final sería menor.
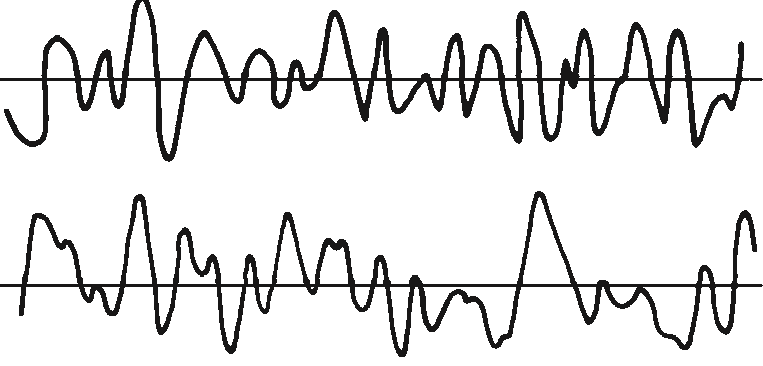
Analizador de vibraciones 13 – Figura 13.10 - Analizador de vibraciones - Correlación de dos vibraciones diferentes
Ahora considere la forma de onda en la Figura 13.11ay la misma forma de onda que se retrasó en el tiempo, Figura 13.11b. Si el tiempo de retraso fuera cero, entonces tendríamos las mismas condiciones que antes, o sea, las formas de onda estarían en fase y la suma final de los productos sería grande. Si el cambio de tiempo entre las dos formas de onda es grande, sin embargo, las formas de onda se ven diferentes y la suma final es pequeña.
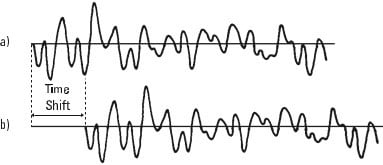
Analizador de vibraciones 13 – Figura 13.11 - Correlación de dos vibraciones idénticas, pero retrasado en el tiempo
Dando un paso más, podemos encontrar el producto promedio para cada retraso de tiempo, dividiendo cada suma final por el número de productos que contribuyen a la misma. Si ahora vemos la gráfica del producto promedio en función del retraso de tiempo, la curva resultante será mayor cuando el retardo de tiempo sea cero y disminuirá a cero a medida que aumente el retardo de tiempo. Esta curva se denomina función de correlación automática de forma de onda.. Es una gráfica de la similitud (o correlación) entre una forma de onda y sí mismo, dependiendo del cambio de hora.
La función de autocorrelación es más fácil de entender si miramos algunos ejemplos. El ruido aleatorio que se muestra en la Figura 13.12 no es similar a sí mismo con ningún retraso de tiempo (por eso es aleatorio) por lo que su autocorrelación tiene solo un pico en el punto de 0 tiempo de retardo.
una) Grabación temporal de ruido aleatorio
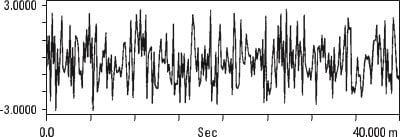
segundo) Correlación automática de ruido aleatorio
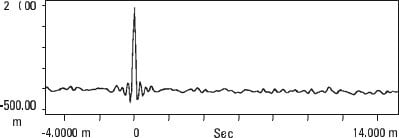
Analizador de vibraciones 13 – Figura 13.12 - Analizador de vibraciones - Correlación de ruido aleatorio
El ruido pseudoaleatorio ( tramos de ruido aleatorio repetidos periódicamente), sin embargo, repite periódicamente, así que cuando el tiempo de demora es igual a un múltiplo del período, La autocorrelación se repite exactamente como en la Figura 13.13.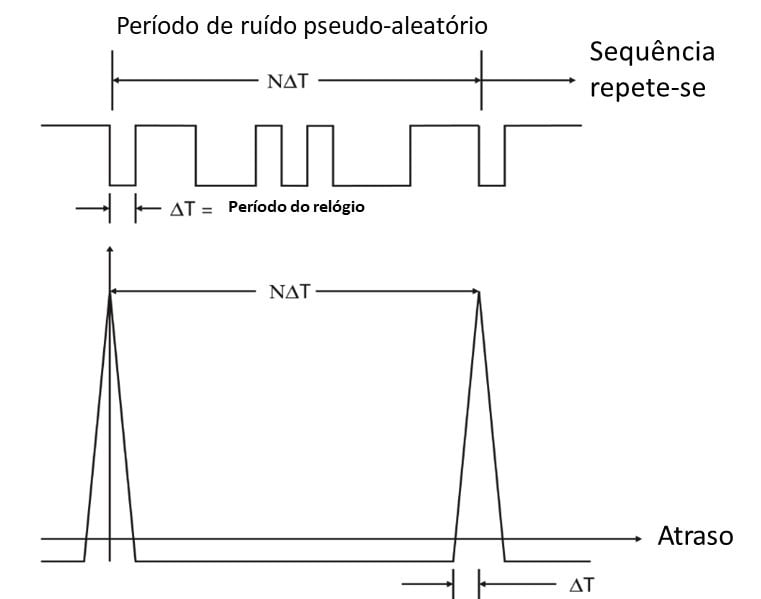
Analizador de vibraciones 13 – Figura 13.13 - Analizador de vibraciones - Correlación de ruido pseudoaleatorio
Ambos son casos especiales de una declaración más general.; la autocorrelación de cualquier forma de onda periódica es periódica y tiene el mismo período que la propia forma de onda.
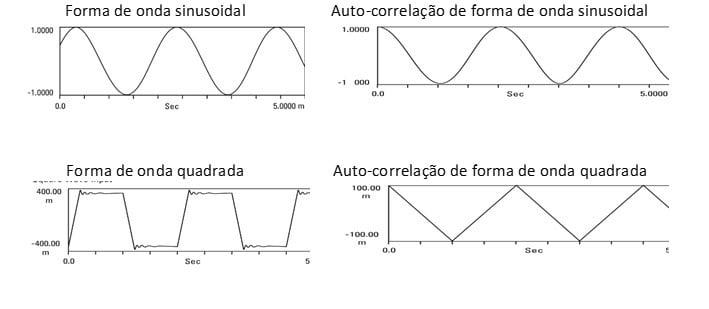Analizador de vibraciones 13 – Figura 13.14 - Analizador de vibraciones - Autocorrelación de ondas periódicas
Esto puede resultar útil cuando se intenta extraer una señal oculta por ruido.. La figura 13.15a muestra lo que parece ser ruido aleatorio., pero en realidad hay una onda sinusoidal de bajo nivel enterrada en ella. Podemos ver esto en la Figura 13.15b, donde tenemos 100 promedios de la autocorrelación de esta señal. El ruido se convirtió en el pico alrededor de un cambio de tiempo cero, mientras que la autocorrelación de la onda sinusoidal es claramente visible, repitiendo con el período de onda sinusoidal. Dado que puede transformar cualquier forma de onda de dominio a tiempo en el dominio de frecuencia, uno puede preguntar cuál es la transformación de frecuencia de la función de autocorrelación? Resulta que es la magnitud al cuadrado del espectro de entrada.. tan, realmente no hay información nueva en la función de autocorrelación, teníamos la misma información en el espectro de la señal. pero, como siempre, Un cambio de perspectiva entre estos dos dominios a menudo aclara los problemas.. En general, señales impulsivas como la causada por una falla en un rodamiento o un engranaje, aparecer mejor en las mediciones de correlación, mientras que las señales con varias ondas sinusoidales de diferentes frecuencias, vibraciones estructurales y maquinaria rotativa, son más claros en el dominio de la frecuencia.
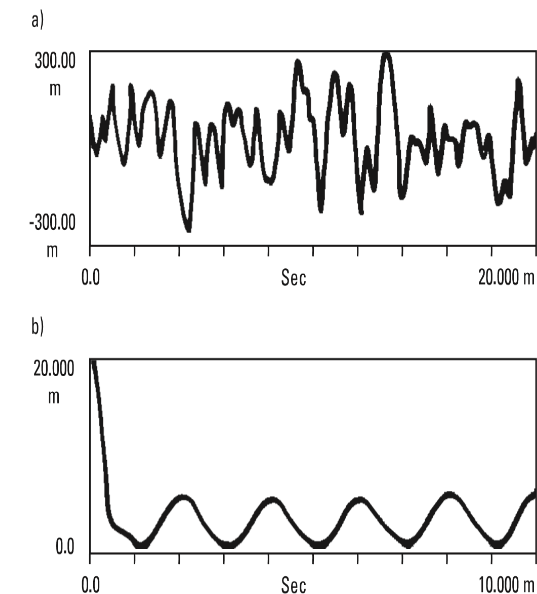Analizador de vibraciones 13 – Figura 13.15 - Analizador de vibraciones - Autocorrelación de onda sinusoidal sumergida en ruido aleatorio
13.7 Analizador de vibraciones 13 - Correlación cruzada entre dos canales
Si la autocorrelación se centra en la similitud entre una señal y una versión de sí misma, entonces es razonable suponer que se puede utilizar la misma técnica para medir la similitud entre dos formas de onda no idénticas. Esto se llama función de correlación cruzada.. Si la misma señal está presente en ambas formas de onda, se reforzará en la función de correlación cruzada, mientras que cualquier ruido no correlacionado se reducirá. En muchos problemas, esta técnica se puede utilizar para eliminar el ruido contaminante de la respuesta mediante correlación cruzada..
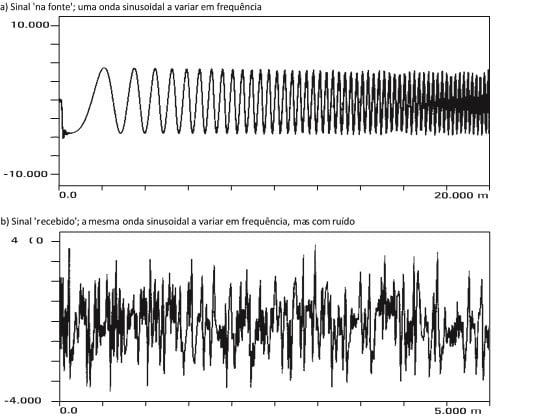do) Resultado de la correlación cruzada de señales transmitidas y recibidas. La distancia desde el lado izquierdo hasta el pico representa un retraso de transmisión..
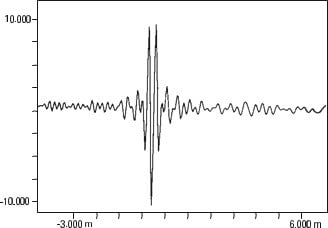Analizador de vibraciones 13 – Figura 13.16 - Analizador de vibraciones - Correlación automática cruzada de dos señales diferentes pero donde existe la misma forma de onda
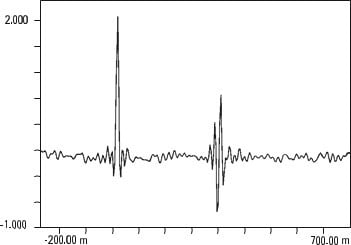
Analizador de vibraciones 13 – Figura 13.17 - Analizador de vibraciones - Correlación cruzada automática de dos señales distintas, pero donde hay la misma forma de onda repetida dos veces
13.7 Analizador de vibraciones 13 - La presentación circular
engranajes, Los rodillos de presión y los cojinetes son ejemplos de piezas de máquinas en las que las vibraciones están asociadas con defectos de forma.. Incluso sabiendo esto, la mayor parte del tiempo al observar la forma de onda para confirmar cualquier diagnóstico, la presentación más utilizada es una función del tiempo. Esta presentación es, indudablemente esencial, La presentación circular es a menudo un complemento útil y poco conocido para los analistas de vibraciones..
13.7.1. En que consiste la presentación circular
Si, en una rotación de un eje, se desplaza en un ángulo de 360º porque no representa las vibraciones correspondientes en un círculo en lugar de representarlas en el tiempo? De esta manera, los defectos de forma asociados con una posición determinada, siempre aparecerán en el mismo lugar, lo que a menudo facilita su identificación y hace que esta herramienta sea una importante ayuda para el diagnóstico.. Siguiente en la figura 13.18, se puede ver la presentación circular de la forma de onda en aceleración de las vibraciones de un rollo con defectos de perfil.
Analizador de vibraciones 13 – Figura 13.18 - Analizador de vibraciones - Visualización circular de las vibraciones de un rollo de una máquina de papel con un defecto de perfil
13.7.2. Técnicas de implementación para presentación circular
Hay varias posibilidades para este enfoque de la representación de vibraciones., a saber:
- Forma de onda simple
- Con la media sincrónica de la forma de onda
- Con forma de onda envolvente y retención de picos ( PeakVue)
13.7.2.1 - La forma de onda
Esta es la forma más simple de representación circular y para hacerlo, solo tenga la velocidad de rotación exacta del eje, lo que normalmente es accesible. Por sí solo, a menudo es difícil de interpretar debido a la interferencia de otras fuentes de vibración..
13.7.2.2 Con la media sincrónica de la forma de onda
La presentación circular de las vibraciones medidas con la media síncrona de la forma de onda permite, por ejemplo, ver el perfil de cada rollo de una máquina de papel, identificar claramente el generador de vibraciones, y causar problemas de calidad en el papel.
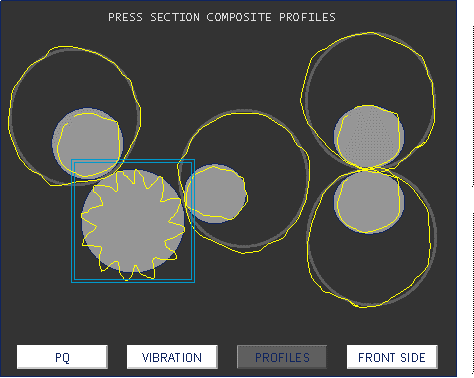Analizador de vibraciones 13 – Figura 13.19 - Analizador de vibraciones - Representación circular de las vibraciones medidas, con la media síncrona de la forma de onda en los rodillos de prensa de la máquina de papel, donde se puede ver qué rodillo tiene la superficie que provoca vibraciones
13.7.2.3 Forma de onda envolvente y retención de picos (PeakVue)
La forma de onda PeakVue también se puede mostrar en forma circular como se muestra en la Figura 13.20
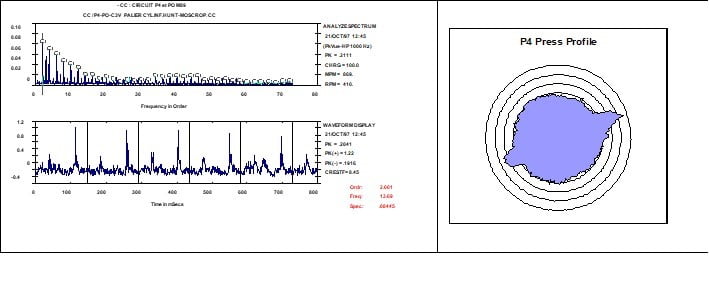Analizador de vibraciones 13 – Figura 13.20 - Analizador de vibraciones - PeakVue Spectrum y Waveform y respectiva representación circular de un rollo de una prensa de máquina de papel con dos defectos de forma en su superficie.
La ventaja que tiene esta técnica, relativo al promedio sincrónico, no es necesario un sensor taquimétrico. Efectivamente, PeakVue es una medida a altas frecuencias y estas se disipan en la estructura de la máquina., no hay fenómeno de interferencia entre los diferentes puntos de medición. En otras palabras, las vibraciones medidas en un punto son exclusivamente las de ese punto.
Ver algunos ejemplos de aplicación de esta técnica Haga clic aquí.
