Analizador de vibraciones 1 – La relación entre tiempo y frecuencia.
Seguidamente, en analizador de vibraciones 1, revisamos la relación entre tiempo y frecuencia, en un analizador de vibraciones al realizar vibraciones de medición. tan, este artículo es parte de una serie de artículos que explican cómo funciona un analizador de vibraciones.
en realidad, cuando llevamos a cabo Análisis de vibraciones, necesitamos entender cómo funciona un analizador. Por eso, aquí presentamos los conceptos de análisis de señales digitales, implementado en un analizador FFT. Para que sea fácil de entender, siempre se presentan desde el punto de vista del usuario, a través de la observación de los resultados de mantenimiento predictivouna.
Seguidamente, No hay enlace, podemos ver a gama deanalizadores de vibración proporcionado por D4VIB.
Después, en analizador de vibraciones 1, vemos el contenido de esta serie de artículos.
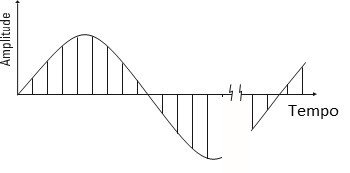
- ¿Cuál es la relación entre tiempo y frecuencia?
- Cómo funciona el muestreo y el escaneo
- Qué es el aliasing y qué efectos tiene
- Cómo se usa y en qué consiste el zoom
- Cómo se utilizan las ventanas de forma de onda
- ¿Cuáles son los promedios para
- ¿Qué es el ancho de banda en tiempo real?
- Para que sirve el procesamiento de superposición ("superposición")
- Que es el seguimiento de pedidos
- Que es el análisis de envolvente
- Las funciones de dos canales en el dominio de la frecuencia
- Para que sirve Orbit
- ¿Cuáles son las funciones de un canal en el dominio del tiempo?
- En qué consiste el Cepstro
- ¿Cuáles son las unidades y escalas del espectro?
1 – Analizador de vibraciones 1 – La relación entre tiempo y frecuencia.
1.1- Cómo funciona FTT y se mueve de vez en cuando
Antes que nada hay que tener en cuenta que con la Transformada Rápida de Fourier ( Transformada rápida de Fourier – FFT) datos de dominio de tiempo pasado, para el dominio de la frecuencia. tan, esto incluso parece fácil de implementar porque eso es lo que queremos que haga un analizador. Sin embargo, veremos que hay muchos factores que complican esta tarea.
Por otro lado, disponer de los resultados rápidamente, tenemos que calcular la FFT automáticamente. Sin embargo, solo podemos calcular la FFT, después de muestrear y digitalizar la forma de onda de entrada.
por lo tanto, este cálculo no se puede realizar de forma continua. tan, esto significa que, el algoritmo transforma bloques completos de datos en el dominio del tiempo, en espectros de frecuencia.
Seguidamente vemos:
- una) La forma de onda en voltios
- segundo) La forma de onda muestreada
- do) El espectro de frecuencias

Figura 1.1 – Las muestras del bloque de tiempo., en el dominio del tiempo, y las líneas en el espectro FFT en el dominio de la frecuencia
Como referido, en ninguno de los dominios hay una representación exacta . Sin embargo, obtenemos una representación de la forma de onda muestreada. De facto, esta presentación está muy cerca de lo previsto.
Seguidamente, ¿Cuál es el espaciado de la muestra en el bloque de tiempo?, para asegurar la resolución deseada, en frecuencia.
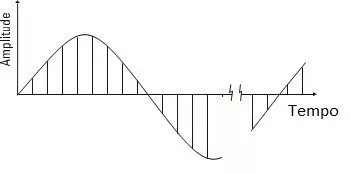
Figura 1.2 Un bloque de tiempo se compone de N muestras equiespaciadas, de la forma de onda analógica de la señal del sensor de vibración, que ingresa al analizador de vibraciones.
1.2 – Analizador de vibraciones 1 – Cómo las muestras de forma de onda forman el bloque de tiempo
En otras palabras, un bloque de tiempo se define como compuesto de:
- Un número N, de muestras de forma de onda,
- Dado que estas muestras son consecutivas,
- Y que estas muestras estén espaciadas uniformemente.
También es necesario, para hacer el cálculo más simple y rápido, el número N es siempre una potencia de 2. tan, es por esto que, analizadores es común encontrar opciones de número de línea como 512, 1024, 2048, 4096, etc.. De facto, estos números son todos poderes de 2.
También es necesario, el bloque de tiempo se transforma como un todo, en uno bloquear lleno de líneas de frecuencia, o sea, en un espectro. tan, por lo tanto, vale la pena señalar que, para calcular cada línea en el dominio de la frecuencia, se requieren todas las muestras del bloque de tiempo.
por lo tanto, es crucial asimilar que la FFT, tiene la propiedad de realizar cálculos de bloques.
Esto es efectivamente necesario, para comprender muchas de las características de un analizador.

Figura 1.3 La FFT se calcula en bloques de muestras de formas de onda..
1.2.1 A medida que el bloque de tiempo se transforma en un espectro
En otras palabras, la FFT no se puede calcular, hasta que se haya adquirido un bloque de tiempo completo.
En otras palabras, Es tan, porque, Como ya fue mencionado, la FFT transforma el bloque de tiempo, como un todo.
Sin embargo, una vez que se completa el cálculo, la muestra más antigua del bloque de tiempo se puede descartar. por lo tanto, cuando se agrega una nueva muestra al comienzo del bloque de tiempo, todas las muestras se mueven en el registro de tiempo y forman un nuevo bloque. tan, tras la adquisición del primer bloque, tenemos un nuevo bloque de tiempo, cada vez que se adquiere una nueva muestra en el dominio del tiempo. De esta forma, cada vez que hay una nueva muestra en el dominio del tiempo, podemos tener un nuevo espectro.

Figura 1.4 Se obtiene un nuevo bloque de muestras de forma de onda después de adquirir cada nueva muestra de forma de onda.
Siendo así, hasta que adquiera un bloque de tiempo completo, no tenemos un espectro valido. Después de este, en el espectro en pantalla del analizador de vibraciones hay cambios rápidos.
Cabe señalar que la presentación de un nuevo espectro, para cada nueva muestra en el bloque de tiempo, es generalmente información que varía con una velocidad excesiva. De hecho esto, muchas veces, daría como resultado la presentación de miles de espectros por segundo.
De facto, al frente, en las secciones sobre el ancho de banda en tiempo real (7) mi procesamiento de superposición (8), Existen diversas implicaciones de la velocidad con la que un analizador de vibraciones calcula la FFT..
1.3 – El número de líneas en el espectro de frecuencias.
Se ha mencionado anteriormente que, el bloque de tiempo consta de N muestras igualmente espaciadas.
tan, otra propiedad FFT, es que transforma estas N muestras en el dominio del tiempo, en N / 2 líneas, uniformemente espaciado, no espetro.
De facto, solo obtienes la mitad de las líneas, porque cada línea de frecuencia, contiene dos piezas de información:
- Una amplitud
- Una fase
Como se sabe, el principio básico de FFT, es que la forma de onda puede descomponerse en una suma de una serie de senos de amplitud y frecuencia variables.
De facto, esto se ve más fácilmente si observamos la relación entre los dominios de tiempo y frecuencia.

Figura 1.5 La relación entre los dominios del tiempo y la frecuencia..
Efectivamente hasta ahora, está implícito que, para reconstruir a forma de onda, la amplitud y frecuencia de las ondas sinusoidales contienen toda la información necesaria. Sin duda, es obvio que la fase de cada una de estas ondas, tambien es importante. Por ejemplo, en la figura 1.6, cuando afasede la onda sinusoidal de frecuencia más alta (El fondo), está cambiado, esto da como resultado un cambio importante en la forma de onda original.

Figura 1.6 La fase de los componentes en el dominio de la frecuencia es importante..
1.4 – Cuánto dura el bloque de tiempo
Seguidamente vamos ver que, la frecuencia más baja que se puede ver con el analizador, se basa en la duración del bloque de tiempo.
en realidad, si el período de la señal de entrada es mayor que la duración del bloque de tiempo, no puedes determinar su período. En otras palabras, las frecuencias más bajas no se pueden determinar. por lo tanto, la primera línea del espectro tiene la misma frecuencia, recíproco de la duración del bloque de tiempo.
una) El período de la señal de entrada es igual al bloque de tiempo. Frecuencia observable más baja.

segundo) Al contrario en esta figura, el período de señal de entrada más largo, es más largo que el bloque de tiempo. Por lo tanto, la FFT no puede calcular, las frecuencias más bajas de la señal de entrada.
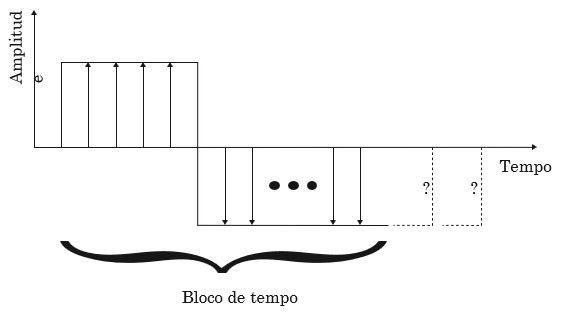
Figura 1.7. O, la inversa de la duración del bloque de tiempo es la frecuencia observable más baja en el espectro.
Además, también hay que tener en cuenta que cero Hertz (corriente continua), hay una línea de frecuencia. De hecho, esta línea representa el promedio de la entrada de la forma de onda..
Se sabe efectivamente que, en el análisis de vibraciones, esta línea rara vez se usa. De facto, para a utilizar, necesitamos un acelerómetro que mida el componente a cero Hz. Efectivamente, cabe señalar que, los acelerómetros piezoeléctricos, normalmente usado, no tengo esta habilidad.
1.5 – Espaciado de líneas en el espectro de frecuencias
por lo tanto, en el espectro de frecuencias, el espacio entre dos líneas consecutivas es el recíproco de la duración del bloque de tiempo.
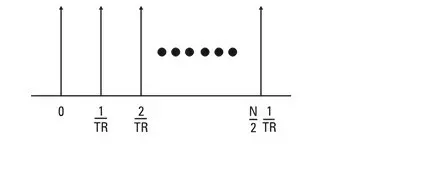
Figura 1.8 – Espaciado de frecuencia de todas las líneas del espectro.
1.6 Porque razón, al mirar espectros de alta resolución, un analizador es más lento
A continuación mencionaremos lo que pasará, cuando le pedimos al analizador que presente un espectro de alta resolución.
se debe notar que, debido a que la resolución es alta, el valor del rango de frecuencia corresponde a un número relativamente pequeño. tan, la duración del bloque de tiempo que se adquiere para calcular el espectro, cual es su reverso, es relativamente grande.
De este modo, para presentar el primer espectro, el analizador tardará un tiempo relativamente largo. De facto, esto se debe a que vas a adquirir un bloque de larga duración.
En otras palabras, es más rápido adquirir espectros de baja resolución que espectros de alta resolución.
en realidad, hay que tener en cuenta que la velocidad de cálculo del analizador no tiene nada que ver con esta característica.
De facto, esta característica es intrínseca a la fórmula de cálculo FFT.
1.7 – ¿Cuál es la frecuencia máxima del espectro??
Ya hemos visto que en un espectro hay N / 2 líneas, espaciados. También sabemos que, el valor de este espaciado es igual al recíproco de la duración del bloque de tiempo. Entonces tienes que, para determinar la frecuencia más alta que podemos ver en un espectro, se utiliza esta fórmula:
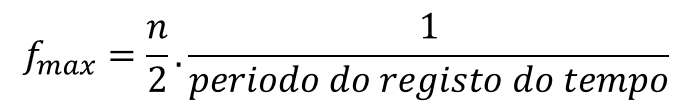
Siendo así, tenemos que el rango de frecuencia del analizador de vibraciones está determinado por la frecuencia de muestreo del bloque de tiempo.
En otras palabras, cuando se le pide a un analizador que calcule un espectro con un determinado máximo , con un cierto número de líneas, se está definiendo simultáneamente:
- La resolución deseada en frecuencia.
- La duración del bloque de tiempo.
Se sabe efectivamente que , el número de líneas en el espectro también implica un cierto número de muestras en el bloque de tiempo. Para hacer esto, durante la duración del bloque, el analizador varía la frecuencia de muestreo para que tenga N muestras.
De esta forma, para alcanzar las frecuencias más altas, el analizador de muestras más rápidamente.
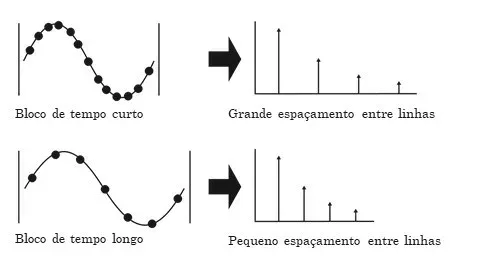
Figura 1.9 – El rango de frecuencia de los analizadores de vibraciones está determinado por la frecuencia de muestreo del bloque de tiempo.
Si desea ver una presentación del tema tratado en Vibration Analyzer 1, Haga clic aquí.