Analisador de vibrações 13 – Funções de um canal no tempo
Analisador de vibrações 13
O tema específico tratado em analisador de vibrações 13, consiste nas funções de um canal no domínio do tempo num analisador de vibrações.
Quando se efetua análise de vibrações, no âmbito de um programa de manutenção preditiva, para se tirar partido de todo o potencial de um analisador de vibrações, é necessário compreender o seu modo de funcionamento. Por isso, aqui são apresentados os conceitos de análise digital de sinal, implementados atualmente num analisador de vibrações FFT, do ponto de vista do utilizador.
Começa-se por apresentar as propriedades do Fast Fourier Transform (FFT) em que os Analisadores de Vibrações são baseados. Em seguida, mostra-se como essas propriedades FFT podem causar algumas características indesejáveis na análise do espectro, como aliasing e fugas (leakage). Tendo apresentado uma dificuldade potencial com o FFT, mostra-se quais soluções são usadas para tornar os analisadores de vibrações em ferramentas práticas. O desenvolvimento desse conhecimento básico das características do FFT torna simples obter bons resultados com um analisador de vibrações numa ampla gama de problemas de medição.
Aqui pode-se ver a gama de analisadores de vibrações disponibilizados pela D4VIB.
- Qual é a relação entre tempo e frequência
- Como funciona a amostragem e digitalização
- O que é o Aliasing e que efeitos tem
- Em se usa e em que consiste o zoom
- Como se usam as janelas na forma de onda
- Para que servem as médias
- O que é a largura de banda em tempo real
- Para que serve o processamento em sobreposição (“overlap”)
- Em que consiste o seguimento de ordens
- O que é a análise do envelope
- As funções de dois canais no domínio da frequência
- O que é para que serve a Órbita
- Quais são as funções de um canal no domínio do tempo
- Em que consiste o Cepstro
- Quais são as unidades e escalas do espetro
13 – Analisador de vibrações 13 – Funções de um canal no domínio no tempo
13.1 Analisador de vibrações – A medição básica da amplitude da forma de onda
A amplitude da vibração, que é a característica que descreve a sua severidade, pode ser medida de diversas maneiras. Na figura a seguir apresentada, pode-se ver a relação entre a Amplitude Pico-Pico, o Pico, a Média e o Nível Eficaz (RMS).
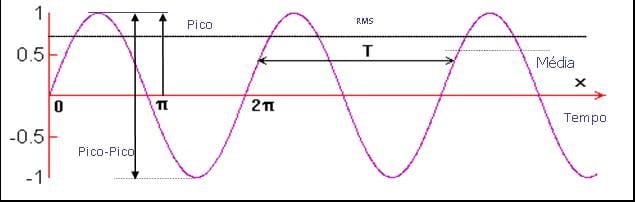Analisador de vibrações 13 – Figura 13.1 Analisador de vibrações – O nível RMS, o pico e o pico-pico
O valor Pico-Pico é importante na medida em que indica a máxima amplitude da vibração, o que é um parâmetro importante quando se trata de saber por exemplo, deslocamentos máximos em máquinas ferramentas ou em medidas efetuadas com transdutores de deslocamento.
O Valor Eficaz (RMS) é o mais frequentemente usado porque toma em conta um determinado intervalo de tempo de medida e dá um valor que está diretamente relacionado com a energia da vibração, ou seja, a sua capacidade destrutiva; é, portanto, um valor médio.
Na figura a seguir apresentada podem-se ver três formas de onda com a mesma amplitude pico e com diferentes valores eficazes. Numa surge um impulso sobreposto a um seno, outra é um seno, outra é um seno truncado.
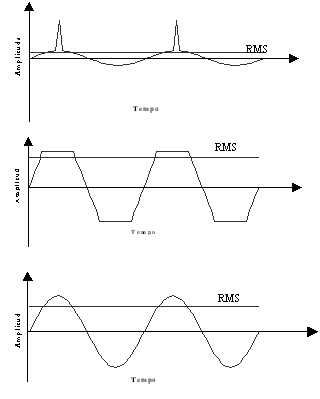Analisador de vibrações 13 – Figura 13.2 – Analisador de vibrações – Três formas de onda com a mesma amplitude pico e com diferentes valores eficazes
Os impulsos que se podem observar na primeira forma de onda, da figura anterior, se ocorressem numa máquina rotativa corresponderiam a choques. A medição da amplitude pico deteta melhor os choques ou qualquer outro tipo de fenómeno impulsivo, que a medição de amplitude RMS, devido ao facto desta última ser um valor médio num determinado intervalo de tempo enquanto o valor pico ser, por definição, o máximo do sinal no tempo. Para medir vibrações sem impulsos a amplitude eficaz (RMS) é mais indicada devido a dar um valor médio. Para medir vibrações sinusoidais, tanto faz, porque existe uma relação fixa entre a amplitude Pico e a RMS.
13.2 O Fator crista
O Factor Crista é o resultado da divisão entre o Valor Pico e o Valor RMS da vibração e é uma técnica para caracterizar a “impulsividade” existente numa forma de onda.
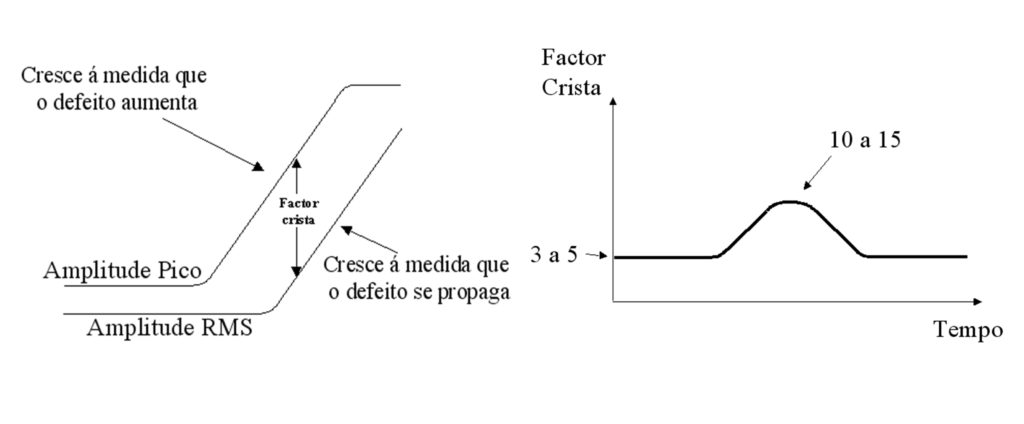Analisador de vibrações 13 – Figura 13.3 – Analisador de vibrações – O fator crista
As curvas na figura acima mostram uma evolução típica do Factor Crista à medida que a condição de funcionamento do rolamento se deteriora. Inicialmente, existe uma razão relativamente constante entre o valor pico e o valor RMS. O valor pico crescerá normalmente até um certo limite. À medida que o rolamento se deteriora, mais impulsos vão ser gerados por cada passagem das esferas, influenciando finalmente os valores RMS, mesmo que a amplitude individual de cada pico não seja maior. Para o fim da vida do rolamento, o Factor Crista pode ter descido para o seu valor original, mesmo que, entretanto, os valores pico e RMS tenham crescido consideravelmente. A melhor maneira para apresentar os resultados das medidas é o apresentado; os valores Pico e RMS no mesmo gráfico, com o Factor Crista inferido a partir da diferença entre as duas curvas.
13.3 O Kurtosis
A Kurtosis é um indicador estatístico da ocorrência de grandes picos numa forma de onda (impulsividade). No mundo real, muitos tipos de vibração são caracterizados por sinais com alto valor de Kurtosis (em relação ao sinal aleatório gaussiano). O potencial de fadiga e dano dessas vibrações é maior do que uma replicação gaussiana pura. O Kurtosis pode ser expresso como um valor normalizado “K” dividindo o quarto momento estatístico dividido pelo quadrado do segundo momento estatístico. A equação abaixo mostra o cálculo do Kurtosis para N amostras.
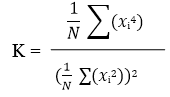
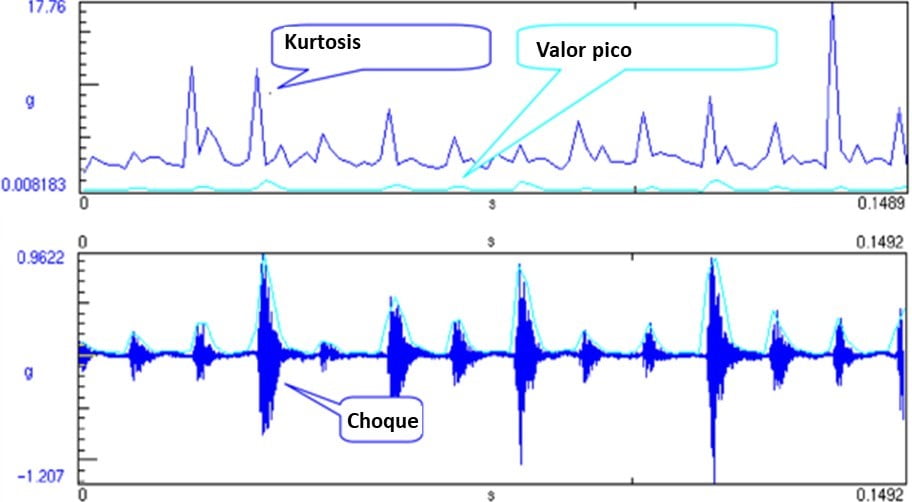
Analisador de vibrações 13 – Figura 13.4 – Analisador de vibrações – Forma de onda, valor pico e Kurtosis
13.4 A assimetrias da amplitude da forma de onda
Observar a simetria dos dados da forma de onda, acima e abaixo do eixo da linha central, é importante. Dados simétricos indicam que o movimento da máquina é uniforme em cada lado da posição central. Dados não simétricos da forma de onda do tempo indicam que o movimento é restringido possivelmente por desalinhamento, fricção ou outra força externa.
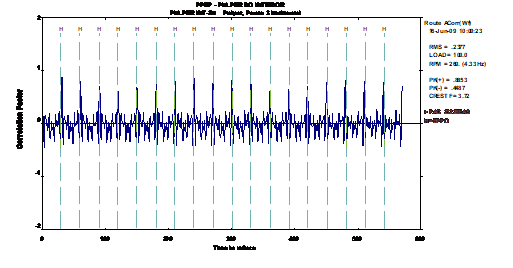Analisador de vibrações 13 – Figura 13.5 – Analisador de vibrações – Forma de onda assimétrica gerada pelos impactos num rolamento
13.5 A média síncrona da forma de onda
Como foi detalhadamente referido em 6.3, esta técnica consiste na realização de medições da forma de onda, sincronizadas com a rotação de um dos veios e execução de uma média dessas medidas. Como resultado desta sincronização os eventos assíncronos com a realização da média, tendem para zero, enquanto os síncronos se tornam mais visíveis. Portanto, a parte periódica da entrada será sempre exatamente a mesma em cada bloco de tempo que tomamos, enquanto o ruído, é claro, variará. Se juntarmos uma série desses blocos de tempo acionados pelo tacómetro e dividir pelo número de blocos que tomamos, vamos calcular o que chamamos de média linear no domínio do tempo. Com esta técnica conseguimos eliminar da forma de ondas as vibrações que não estão relacionadas com o veio nde está o tacómetro, como por exemplo se pode ver a seguir , na Figura 13.6 para identificar uma fenda numa engrenagem.
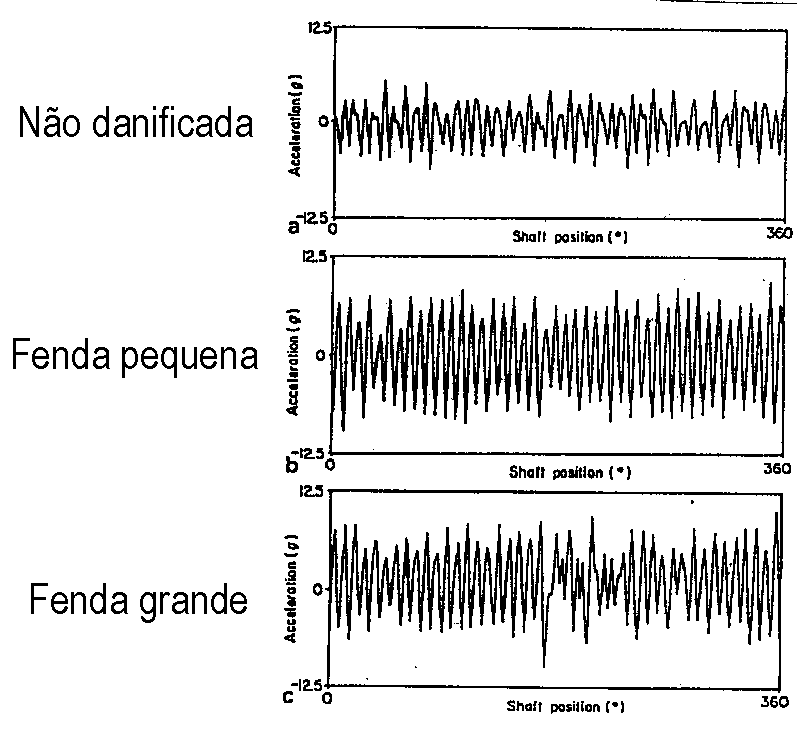
Analisador de vibrações 13 – Figura 13.6 – Analisador de vibrações – Deteção de fendas em engrenagens através da Média Síncrona da Forma de Onda
Para a implementação desta técnica é requerida a existência de um sensor tacométrico que informe permanentemente o equipamento de medida sobre a velocidade de rotação do veio onde estão a ser efetuadas as medições de vibrações. Esta técnica tem tradicionalmente aplicação em engrenagens complexas e de alta responsabilidade como sejam as dos helicópteros para determinação de defeitos em dentes, e em prensas de máquinas de papel ou trens de laminagem para determinar a origem das vibrações de forma a evitar problemas de qualidade. Ela permite, por exemplo, em dois rolos de uma prensa a rodarem à mesma velocidade, distinguir as vibrações geradas por um, das vibrações geradas pelo outro, como é ilustrado na Figura 13.7
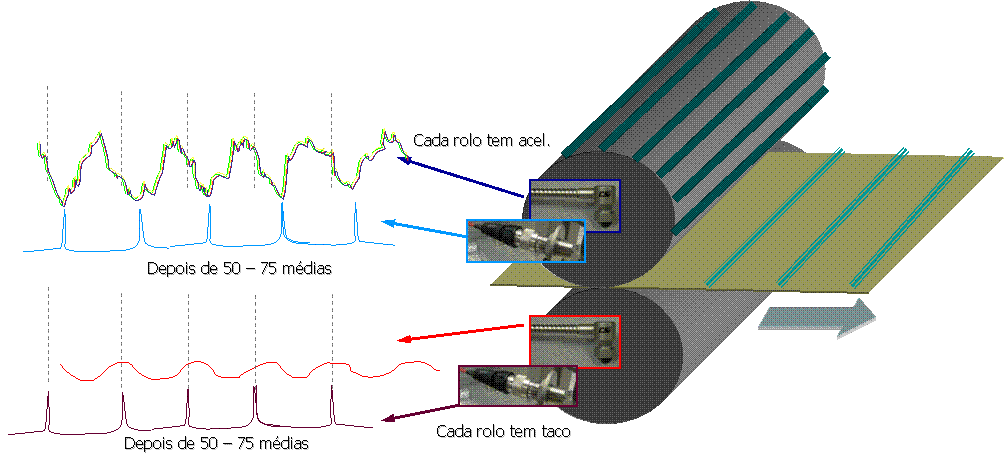Analisador de vibrações 13 – Figura 13.7 – Implementação da média síncrono em rolos de prensa de máquina de papel
A sincronização das medidas funciona como um filtro que nos permite observar exclusivamente/separar as vibrações de uma fonte das outras.
13.6 Analisador de vibrações 13 – A autocorrelação
A auto-correlação é uma técnica de correlação que envolve apenas um sinal, e fornece informações sobre a periodicidade do sinal no domínio no tempo. A auto-correlação, surge assim, como uma alternativa à análise espectral. As principais características desta função são:
• a capacidade de identificar eventos de baixa repetição,
• a capacidade de identificar e separar eventos periódicos de eventos aleatórios.
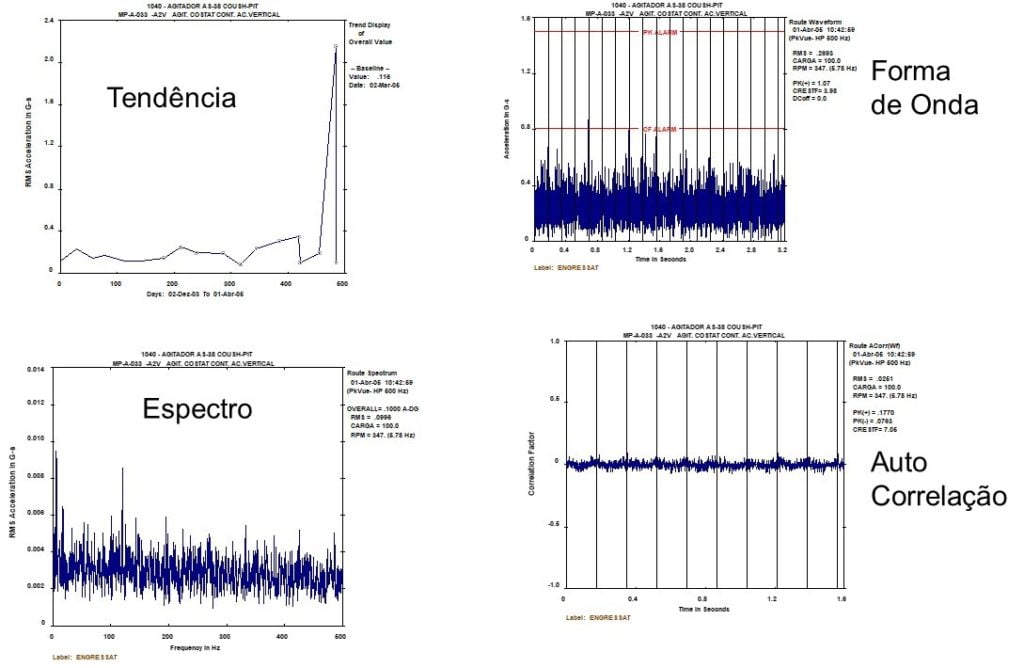
Analisador de vibrações 13 – Figura 13.8 – Analisador de vibrações – Aplicação da função de auto-correlação para identificar a ausência de periodicidade, ou seja, o caracter aleatório de um sinal de vibrações quando ocorre um problema de lubrificação num rolamento
Um analisador de vibrações tem normalmente a capacidade de exibir o registo de tempo no seu ecrã. Esta é a mesma forma de onda que veríamos com um osciloscópio, uma visão de domínio temporal da entrada. Mas há outras medições de domínio de tempo que um Analisador de Vibrações também pode fazer. Estas são chamadas medidas de correlação. Vamos começar esta secção definindo a correlação e, em seguida, mostraremos como fazer estas medições com um Analisador de Vibrações.
A correlação é uma medida da semelhança entre duas quantidades. Para compreender a correlação entre duas formas de onda, comece-se por multiplicar estas formas de onda em cada instante e somar todos os produtos. Se, como na Figura 13.9, as formas de onda forem idênticas, cada produto é positivo e a soma resultante é grande.
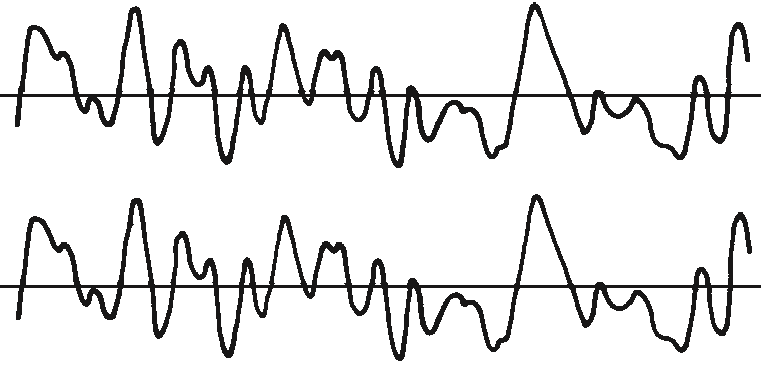Analisador de vibrações 13 – Figura 13.9 – Analisador de vibrações – Correlação de duas vibrações idênticas
Se, no entanto, tal como na Figura 13.10, os dois registos forem diferentes, então alguns dos produtos seriam positivos e alguns seriam negativos. Haveria uma tendência para os produtos cancelarem, pelo que a soma final seria menor.
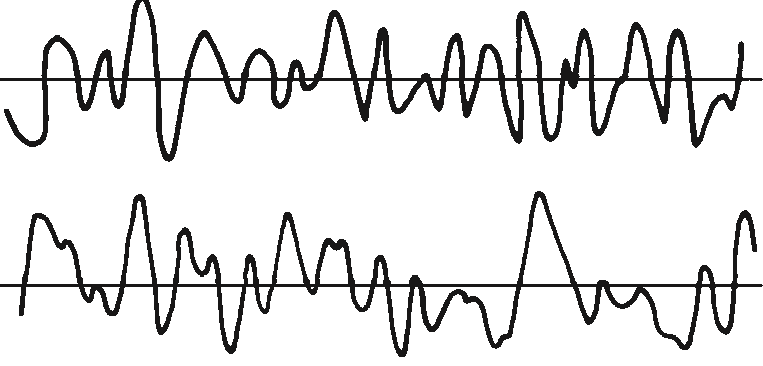
Analisador de vibrações 13 – Figura 13.10 – Analisador de vibrações – Correlação de duas vibrações diferentes
Agora considere-se a forma de onda na Figura 13.11a e a mesma forma de onda que se atrasou no tempo, Figura 13.11b. Se o atraso do tempo fosse zero, então teríamos as mesmas condições que antes, ou seja, as formas de onda estariam em fase e a soma final dos produtos seria grande. Se a mudança de tempo entre as duas formas de onda for grande, no entanto, as formas de onda parecem diferentes e a soma final é pequena.
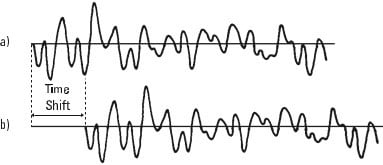
Analisador de vibrações 13 – Figura 13.11 – Correlação de duas vibrações idênticas, mas desfasadas no tempo
Indo um passo mais longe, podemos encontrar o produto médio para cada atraso no tempo, dividindo cada soma final pelo número de produtos que contribuem para o mesmo. Se agora virmos o gráfico do produto médio em função do atraso de tempo, a curva resultante será maior quando o atraso no tempo for zero e diminuirá para zero à medida que o atraso de tempo aumenta. Esta curva é chamada a função de correlação automática da forma de onda. É um gráfico da semelhança (ou correlação) entre uma forma de onda e si mesmo, em função da mudança de tempo.
A função de auto-correlação é mais fácil de entender se olharmos para alguns exemplos. O ruído aleatório mostrado na Figura 13.12 não é semelhante a si mesmo com qualquer quantidade de atraso de tempo (é por isso que é aleatório) pelo que a sua auto-correlação tem apenas um pico no ponto de 0 atraso de tempo.
a) Registo temporal de ruído aleatório
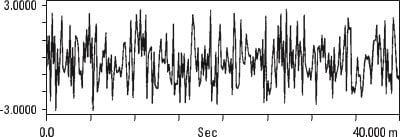
b) Correlação automática de ruído aleatório
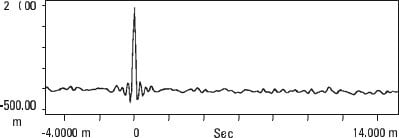
Analisador de vibrações 13 – Figura 13.12 – Analisador de vibrações – Correlação de ruído aleatório
O ruído pseudoaleatório ( troços de ruído aleatório repetido periodicamente), no entanto, repete-se periodicamente, pelo que quando o atraso no tempo é igual a um múltiplo do período, a auto-correlação repete-se exatamente como na Figura 13.13.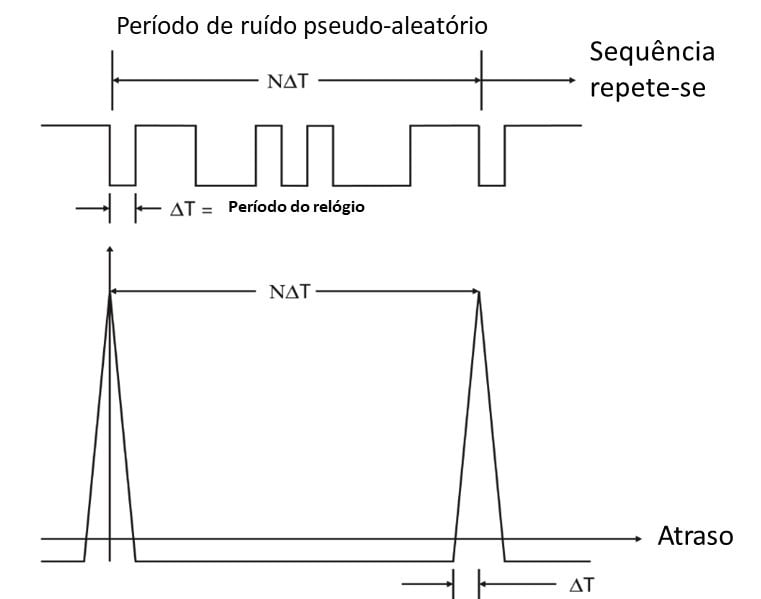
Analisador de vibrações 13 – Figura 13.13 – Analisador de vibrações – Correlação de ruído pseudo-aleatório
Estes são ambos casos especiais de uma declaração mais geral; a auto-correlação de qualquer forma de onda periódica é periódica e tem o mesmo período que a própria forma de onda.
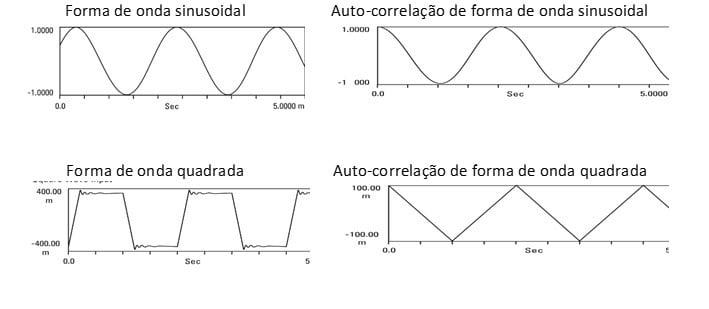Analisador de vibrações 13 – Figura 13.14 – Analisador de vibrações – Auto-correlação de ondas periódicas
Isto pode ser útil quando se tenta extrair um sinal escondido pelo ruído. A figura 13.15a mostra o que parece ser ruído aleatório, mas na verdade há uma onda sinusoidal de baixo nível enterrada nele. Podemos ver isso na Figura 13.15b, onde temos 100 médias da auto-correlação deste sinal. O ruído tornou-se o pico em torno de uma mudança de tempo de zero, enquanto a auto-correlação da onda sinusoidal é claramente visível, repetindo-se com o período da onda sinusoidal. Uma vez que se pode transformar qualquer forma de onda de domínio em tempo no domínio da frequência, pode-se perguntar-se qual é a transformação de frequência da função de auto-correlação? Acontece que é a magnitude ao quadrado do espectro da entrada. Assim, não há realmente nenhuma informação nova na função de autocorrelação, teve-se a mesma informação no espectro do sinal. Mas, como sempre, uma mudança de perspetiva entre estes dois domínios muitas vezes esclarece os problemas. Em geral, os sinais impulsivos como o originado numa avaria num rolamento ou numa engrenagem, aparecem melhor nas medições de correlação, enquanto os sinais com várias ondas sinusoidais de diferentes frequências, como vibrações estruturais e de máquinas rotativas, são mais claros no domínio da frequência.
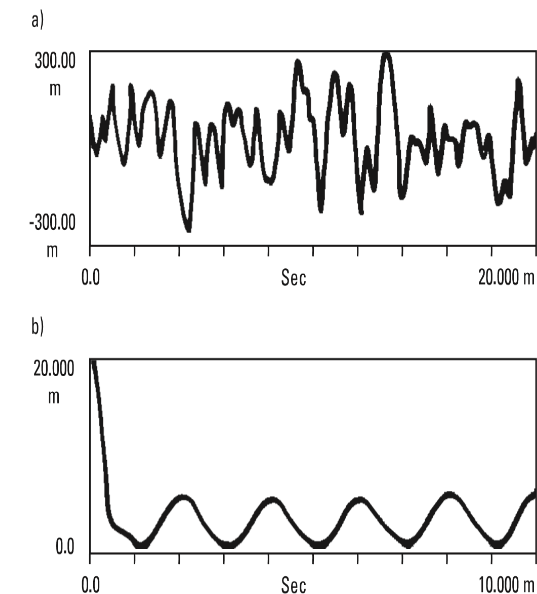Analisador de vibrações 13 – Figura 13.15 – Analisador de vibrações – Auto-correlação de onda sinusoidal submergida em ruído aleatório
13.7 Analisador de vibrações 13 – Correlação Cruzada entre dois canais
Se a auto-correlação se foca com a semelhança entre um sinal e uma versão de si mesma, então é razoável supor que a mesma técnica pode ser usada para medir a semelhança entre duas formas de onda não idênticas. Isto é chamado a função de correlação cruzada. Se o mesmo sinal estiver presente em ambas as formas de onda, será reforçado na função de correlação cruzada, enquanto qualquer ruído não correlacionado será reduzido. Em muitos problemas de esta técnica pode ser usada para remover o ruído contaminante da resposta através da correlação cruzada.
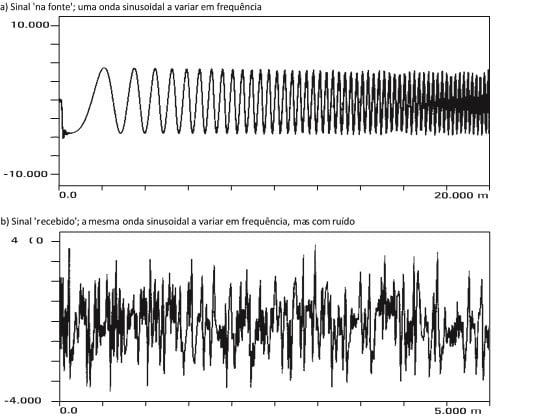c) Resultado da correlação cruzada dos sinais transmitidos e recebidos. A distância do lado esquerdo ao pico representa um atraso de transmissão.
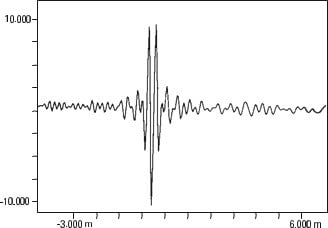Analisador de vibrações 13 – Figura 13.16 – Analisador de vibrações – Auto-correlação-cruzada de dois sinais distintos mas onde existe a mesma forma de onda
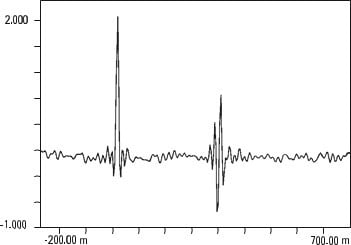
Analisador de vibrações 13 – Figura 13.17 – Analisador de vibrações – Auto-correlação-cruzada de dois sinais distintos, mas onde existe a mesma forma de onda repetida duas vezes
13.7 Analisador de vibrações 13 – A apresentação circular
Engrenagens, rolamentos e rolos de prensas são exemplos de órgãos de máquinas em que as vibrações estão associadas a defeitos de forma. Mesmo sabendo isto, a maioria das vezes quando se observa a forma de onda para confirmar um qualquer diagnóstico, a apresentação mais utilizada é em função do tempo. Sendo esta apresentação, sem dúvida essencial, a apresentação circular é frequentemente um auxiliar útil e pouco conhecido dos analistas de vibrações.
13.7.1. Em que consiste a apresentação circular
Se numa rotação de um veio este percorre um ângulo de 360º porque não representar as vibrações correspondentes num círculo em vez das representar ao longo do tempo? Desta forma os defeitos de forma associados a uma determinada posição, surgirão sempre no mesmo local tornando-se frequentemente mais fácil a sua identificação e tornando-se esta ferramenta um importante auxiliar de diagnóstico. A seguir na Figura 13.18, pode-se ver a apresentação circular da forma de onda em aceleração das vibrações de um rolo com defeitos de perfil.
Analisador de vibrações 13 – Figura 13.18 – Analisador de vibrações – Apresentação circular das vibrações de um rolo de uma máquina de papel com defeito de perfil
13.7.2. Técnicas de implementação da apresentação circular
Existem diversas possibilidades para esta abordagem à representação das vibrações, nomeadamente:
– Forma de onda simples
– Com a média síncrona da forma de onda
– Com forma de onda do envelope e retenção do pico ( PeakVue)
13.7.2.1 – A forma de onda
Esta é a forma mais simples da representação circular e para a efectuar basta dispor da exacta velocidade de rotação do veio, o que normalmente é acessível. Por si só é frequentemente de difícil interpretação devido à interferência de outras fontes de vibrações.
13.7.2.2 Com a média síncrona da forma de onda
A apresentação circular das vibrações medidas com a média síncrona da forma de onda permite, por exemplo, visualizar o perfil de cada rolo de uma máquina de papel, identificando claramente o gerador de vibrações, e causador de problemas de qualidade no papel.
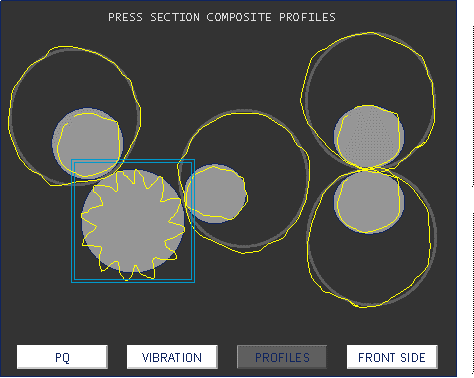Analisador de vibrações 13 – Figura 13.19 – Analisador de vibrações – Representação circular de vibrações medidas, com a média síncrona da forma de onda em rolos de prensa de máquina de papel, onde se vê qual o rolo tem a superfície que origina vibrações
13.7.2.3 Forma de onda do envelope e retenção do pico (PeakVue)
A forma de onda do PeakVue também pode ser apresentada em forma circular como se pode ver na Figura 13.20
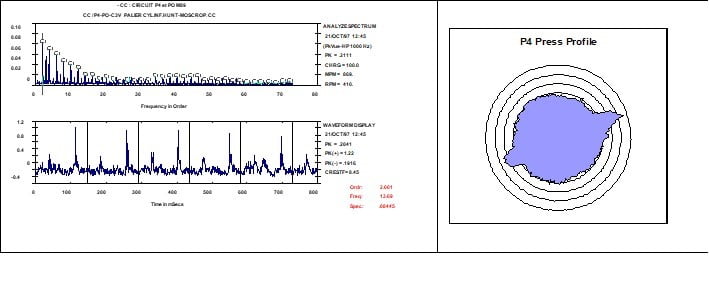Analisador de vibrações 13 – Figura 13.20 – Analisador de vibrações – Espectro e Forma de Onda de PeakVue e respetiva representação circular de um rolo de uma prensa de máquina de papel com dois defeitos de forma na sua superfície.
A vantagem que esta técnica apresenta, relativamente à média síncrona, é a de não necessitar de sensor tacométrico. Efetivamente como o PeakVue é uma medição nas altas frequências e estas são dissipadas na estrutura da máquina, não ocorre o fenómeno de interferência entre os diversos pontos de medida. Por outras palavras, as vibrações medidas num ponto são exclusivamente as desse ponto.
Para ver alguns exemplos de aplicação desta técnica clique aqui.
